算法题目
#2020学习打卡##C程序设计语言# C语言实现快速排序
C语言 • zkbhj 发表了文章 • 0 个评论 • 1265 次浏览 • 2020-04-23 17:24
关于什么是快速排序，可以参考文章 ：什么是快速排序。里面有介绍快速排序的方法以及和冒泡排序的区别，还有PHP版本实现快速排序的方法。本文章只讨论C语言实现的一种方式。#include <stdio.h>
//快速排序算法(从小到大)
//arr:需要排序的数组，begin:需要排序的区间左边界，end:需要排序的区间的右边界
void quickSort(int *arr,int begin,int end)
{
//如果区间不只一个数
if(begin < end)
{
int temp = arr[begin]; //将区间的第一个数作为基准数
int i = begin; //从左到右进行查找时的“指针”，指示当前左位置
int j = end; //从右到左进行查找时的“指针”，指示当前右位置
//不重复遍历
while(i < j)
{
//当右边的数大于基准数时，略过，继续向左查找
//不满足条件时跳出循环，此时的j对应的元素是小于基准元素的
while(i<j && arr[j] > temp)
j--;
//将右边小于等于基准元素的数填入右边相应位置
arr[i] = arr[j];
//当左边的数小于等于基准数时，略过，继续向右查找
//(重复的基准元素集合到左区间)
//不满足条件时跳出循环，此时的i对应的元素是大于等于基准元素的
while(i<j && arr[i] <= temp)
i++;
//将左边大于基准元素的数填入左边相应位置
arr[j] = arr[i];
}
//将基准元素填入相应位置
arr[i] = temp;
//此时的i即为基准元素的位置
//对基准元素的左边子区间进行相似的快速排序
quickSort(arr,begin,i-1);
//对基准元素的右边子区间进行相似的快速排序
quickSort(arr,i+1,end);
}
//如果区间只有一个数，则返回
else
return;
}
int main()
{
int num[12] = {23,45,17,11,13,89,72,26,3,17,11,13};
int n = 12;
quickSort(num,0,n-1);
printf("排序后的数组为：\n");
// for(int i=0;i<n;i++)
// printf("%d ", num[i]);
int *p = num;
while(n>0) {
n--;
printf("%d ",*p++);
}
return 0;
}
[/i][/i][/i][/i][/i][i][i][i][i]https://github.com/happy-hacki ... ort.c[/i][/i][/i][/i] 查看全部
//快速排序算法(从小到大)
//arr:需要排序的数组，begin:需要排序的区间左边界，end:需要排序的区间的右边界
void quickSort(int *arr,int begin,int end)
{
//如果区间不只一个数
if(begin < end)
{
int temp = arr[begin]; //将区间的第一个数作为基准数
int i = begin; //从左到右进行查找时的“指针”，指示当前左位置
int j = end; //从右到左进行查找时的“指针”，指示当前右位置
//不重复遍历
while(i < j)
{
//当右边的数大于基准数时，略过，继续向左查找
//不满足条件时跳出循环，此时的j对应的元素是小于基准元素的
while(i<j && arr[j] > temp)
j--;
//将右边小于等于基准元素的数填入右边相应位置
arr[i] = arr[j];
//当左边的数小于等于基准数时，略过，继续向右查找
//(重复的基准元素集合到左区间)
//不满足条件时跳出循环，此时的i对应的元素是大于等于基准元素的
while(i<j && arr[i] <= temp)
i++;
//将左边大于基准元素的数填入左边相应位置
arr[j] = arr[i];
}
//将基准元素填入相应位置
arr[i] = temp;
//此时的i即为基准元素的位置
//对基准元素的左边子区间进行相似的快速排序
quickSort(arr,begin,i-1);
//对基准元素的右边子区间进行相似的快速排序
quickSort(arr,i+1,end);
}
//如果区间只有一个数，则返回
else
return;
}
int main()
{
int num[12] = {23,45,17,11,13,89,72,26,3,17,11,13};
int n = 12;
quickSort(num,0,n-1);
printf("排序后的数组为：\n");
// for(int i=0;i<n;i++)
// printf("%d ", num[i]);
int *p = num;
while(n>0) {
n--;
printf("%d ",*p++);
}
return 0;
}
[/i][/i][/i][/i][/i][i][i][i][i]https://github.com/happy-hacki ... ort.c[/i][/i][/i][/i] 查看全部
关于什么是快速排序，可以参考文章 ：什么是快速排序。里面有介绍快速排序的方法以及和冒泡排序的区别，还有PHP版本实现快速排序的方法。本文章只讨论C语言实现的一种方式。
#include <stdio.h>[i][i][i][i]https://github.com/happy-hacki ... ort.c[/i][/i][/i][/i]
//快速排序算法(从小到大)
//arr:需要排序的数组，begin:需要排序的区间左边界，end:需要排序的区间的右边界
void quickSort(int *arr,int begin,int end)
{
//如果区间不只一个数
if(begin < end)
{
int temp = arr[begin]; //将区间的第一个数作为基准数
int i = begin; //从左到右进行查找时的“指针”，指示当前左位置
int j = end; //从右到左进行查找时的“指针”，指示当前右位置
//不重复遍历
while(i < j)
{
//当右边的数大于基准数时，略过，继续向左查找
//不满足条件时跳出循环，此时的j对应的元素是小于基准元素的
while(i<j && arr[j] > temp)
j--;
//将右边小于等于基准元素的数填入右边相应位置
arr[i] = arr[j];
//当左边的数小于等于基准数时，略过，继续向右查找
//(重复的基准元素集合到左区间)
//不满足条件时跳出循环，此时的i对应的元素是大于等于基准元素的
while(i<j && arr[i] <= temp)
i++;
//将左边大于基准元素的数填入左边相应位置
arr[j] = arr[i];
}
//将基准元素填入相应位置
arr[i] = temp;
//此时的i即为基准元素的位置
//对基准元素的左边子区间进行相似的快速排序
quickSort(arr,begin,i-1);
//对基准元素的右边子区间进行相似的快速排序
quickSort(arr,i+1,end);
}
//如果区间只有一个数，则返回
else
return;
}
int main()
{
int num[12] = {23,45,17,11,13,89,72,26,3,17,11,13};
int n = 12;
quickSort(num,0,n-1);
printf("排序后的数组为：\n");
// for(int i=0;i<n;i++)
// printf("%d ", num[i]);
int *p = num;
while(n>0) {
n--;
printf("%d ",*p++);
}
return 0;
}
[/i][/i][/i][/i][/i]
#2020学习打卡##C程序设计语言# 直接插入排序和改进版Shell排序解析
C语言 • zkbhj 发表了文章 • 0 个评论 • 1177 次浏览 • 2020-04-14 17:54
一、直接插入排序
直接插入排序（Straight Insertion Sort）是一种最简单的排序方法，其基本操作是将一条记录插入到已排好的有序表中，从而得到一个新的、记录数量增1的有序表。直接插入排序的时间复杂度为 O(n2)。
实例如下所示：
定义的数组 ： {23,34,56,78,65,90,88,92,18,21}
过程如下所示：
【23】 34 56 78 65 90 88 92 18 21
第 1 次排序结果： 【23 34】 56 78 65 90 88 92 18 21
——用34插入到【23】序列中，34>23，故插入后的顺序是【23，34】
第 2 次排序结果： 【 23 34 56 】78 65 90 88 92 18 21
——用56插入到【23，34】序列中，56>34，故插入后的顺序是【23，34，56】
第 3 次排序结果： 【23 34 56 78】65 90 88 92 18 21
——用78插入到【23，34，56】序列中，78>56，故插入后的顺序是【23，34，56，78】
第 4 次排序结果： 【23 34 56 65 78 】90 88 92 18 21
——用65插入到【23，34，56，78】序列中，65<78，所以78后移一位，和56比较，65>56,故插入后的顺序是【23，34，56，65, 78】
第 5 次排序结果： 【23 34 56 65 78 90 】 88 92 18 21
——用90插入到【23，34，56，65, 78】序列中，78<90 ,故插入后的顺序是【23 34 56 65 78 90 】
第 6 次排序结果： 23 34 56 65 78 88 90 92 18 21
——用88插入到【23 34 56 65 78 90 】序列中，90>88 ,所以90后移一位,故插入后的顺序是【23 34 56 65 78 88 90】
第 7 次排序结果： 23 34 56 65 78 88 90 92 18 21
——用92插入到【23 34 56 65 78 90 】序列中，90<92 ,故插入后的顺序是【23 34 56 65 78 90 92 】
第 8 次排序结果： 18 23 34 56 65 78 88 90 92 21
——用18插入到【23 34 56 65 78 90 92 】序列中，18<92，所以92后移一位，和90比较，90>18,依次后移，直到第一位23，因为18<23, 故插入后的顺序是【18 23 34 56 65 78 88 90 92】
第 9 次排序结果： 18 21 23 34 56 65 78 88 90 92
——用21插入到【23 34 56 65 78 90 92 】序列中，21<92，故92后移一位，和90比较，90>21,依次后移，直到第一位18，因为18<21, 故插入后的顺序是【18 21 23 34 56 65 78 88 90 92】
C语言实现：#include <stdio.h>
//自定义的输出函数
void print(int a, int n ,int i){
printf("%d:",i);
for(int j=0; j<8; j++){
printf("%d",a[j]);
}
printf("\n");
}
//直接插入排序函数
void InsertSort(int a, int n)
{
for(int i= 1; i<n; i++){
if(a < a[i-1]){//若第 i 个元素大于 i-1 元素则直接插入；反之，需要找到适当的插入位置后在插入。
int j= i-1;
int x = a;
while(j>-1 && x < a[j]){ //采用顺序查找方式找到插入的位置，在查找的同时，将数组中的元素进行后移操作，给插入元素腾出空间
a[j+1] = a[j];
j--;
}
a[j+1] = x; //插入到正确位置
}
print(a,n,i);//打印每次排序后的结果
}
}
int main(){
int a[8] = {3,1,7,5,2,4,9,6};
InsertSort(a,8);
return 0;
}
二、Shell排序：直接插入排序算法的一种高速而稳定的改进版本
希尔排序，也称递减增量排序算法，是一种插入排序算法，它出自D.L.Shell，因此而得名。Shell排序又称作缩小增量排序。Shell排序的执行时间依赖于增量序列。
希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。
先取一个小于n的整数d1作为第一个增量，把文件的全部记录分组。所有距离为d1的倍数的记录放在同一个组中。先在各组内进行直接插入排序；然后，取第二个增量d2<d1重复上述的分组和排序，直至所取的增量=1(<…<d2<d1)，即所有记录放在同一组中进行直接插入排序为止。
Shell排序算法的特点
希尔排序是基于插入排序的以下两点性质而提出改进方法的：
插入排序在对几乎已经排好序的数据操作时， 效率高， 即可以达到线性排序的效率[list][*]但插入排序一般来说是低效的， 因为插入排序每次只能将数据移动一位
[/*]
[/list]
时间复杂度：最坏情况下为O(n^2)，平均时间复杂度为O(nlogn)；
空间复杂度：归并排序需要一个大小为1的临时存储空间用以保存合并序列，所以空间复杂度为O(1)
算法稳定性：从上面图片中可以看出，数字5在排序后交换了位置，所以它是不稳定的算法。
例如：12、5、9、34、6、8、33、56、89、0、7、4、22、55、77
具体步骤：
void Shell(int *arr,int len,int gap)
{
for(int i = gap;i < len;i++)
{
int temp = arr;
int j = 0;
for(j = i-gap;j >= 0;j-=gap)
{
if(arr[j] > temp)
{
arr[j+gap] = arr[j];
}
else
{
break;
}
}
arr[j+gap] = temp;
}
}
void Shell_Sort(int *arr,int len)
{
int drr = {5,3,1}; //drr为分的组数，这里5，3，1不固定，但必须相互为素数，且最后数为1
int lend = sizeof(drr)/sizeof(drr[0]);
for(int i = 0;i < lend;i++)
{
Shell(arr,len,drr);
}
}
引用文章：
https://blog.csdn.net/FDk_LCL/java/article/details/90581904
https://www.cnblogs.com/guopengxia0719/p/10520561.html
https://www.cnblogs.com/BaoZiY/p/10931406.html
查看全部
直接插入排序（Straight Insertion Sort）是一种最简单的排序方法，其基本操作是将一条记录插入到已排好的有序表中，从而得到一个新的、记录数量增1的有序表。直接插入排序的时间复杂度为 O(n2)。
实例如下所示：
定义的数组 ： {23,34,56,78,65,90,88,92,18,21}
过程如下所示：
【23】 34 56 78 65 90 88 92 18 21
第 1 次排序结果： 【23 34】 56 78 65 90 88 92 18 21
——用34插入到【23】序列中，34>23，故插入后的顺序是【23，34】
第 2 次排序结果： 【 23 34 56 】78 65 90 88 92 18 21
——用56插入到【23，34】序列中，56>34，故插入后的顺序是【23，34，56】
第 3 次排序结果： 【23 34 56 78】65 90 88 92 18 21
——用78插入到【23，34，56】序列中，78>56，故插入后的顺序是【23，34，56，78】
第 4 次排序结果： 【23 34 56 65 78 】90 88 92 18 21
——用65插入到【23，34，56，78】序列中，65<78，所以78后移一位，和56比较，65>56,故插入后的顺序是【23，34，56，65, 78】
第 5 次排序结果： 【23 34 56 65 78 90 】 88 92 18 21
——用90插入到【23，34，56，65, 78】序列中，78<90 ,故插入后的顺序是【23 34 56 65 78 90 】
第 6 次排序结果： 23 34 56 65 78 88 90 92 18 21
——用88插入到【23 34 56 65 78 90 】序列中，90>88 ,所以90后移一位,故插入后的顺序是【23 34 56 65 78 88 90】
第 7 次排序结果： 23 34 56 65 78 88 90 92 18 21
——用92插入到【23 34 56 65 78 90 】序列中，90<92 ,故插入后的顺序是【23 34 56 65 78 90 92 】
第 8 次排序结果： 18 23 34 56 65 78 88 90 92 21
——用18插入到【23 34 56 65 78 90 92 】序列中，18<92，所以92后移一位，和90比较，90>18,依次后移，直到第一位23，因为18<23, 故插入后的顺序是【18 23 34 56 65 78 88 90 92】
第 9 次排序结果： 18 21 23 34 56 65 78 88 90 92
——用21插入到【23 34 56 65 78 90 92 】序列中，21<92，故92后移一位，和90比较，90>21,依次后移，直到第一位18，因为18<21, 故插入后的顺序是【18 21 23 34 56 65 78 88 90 92】
C语言实现：#include <stdio.h>
//自定义的输出函数
void print(int a, int n ,int i){
printf("%d:",i);
for(int j=0; j<8; j++){
printf("%d",a[j]);
}
printf("\n");
}
//直接插入排序函数
void InsertSort(int a, int n)
{
for(int i= 1; i<n; i++){
if(a < a[i-1]){//若第 i 个元素大于 i-1 元素则直接插入；反之，需要找到适当的插入位置后在插入。
int j= i-1;
int x = a;
while(j>-1 && x < a[j]){ //采用顺序查找方式找到插入的位置，在查找的同时，将数组中的元素进行后移操作，给插入元素腾出空间
a[j+1] = a[j];
j--;
}
a[j+1] = x; //插入到正确位置
}
print(a,n,i);//打印每次排序后的结果
}
}
int main(){
int a[8] = {3,1,7,5,2,4,9,6};
InsertSort(a,8);
return 0;
}
二、Shell排序：直接插入排序算法的一种高速而稳定的改进版本
希尔排序，也称递减增量排序算法，是一种插入排序算法，它出自D.L.Shell，因此而得名。Shell排序又称作缩小增量排序。Shell排序的执行时间依赖于增量序列。
希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。
先取一个小于n的整数d1作为第一个增量，把文件的全部记录分组。所有距离为d1的倍数的记录放在同一个组中。先在各组内进行直接插入排序；然后，取第二个增量d2<d1重复上述的分组和排序，直至所取的增量=1(<…<d2<d1)，即所有记录放在同一组中进行直接插入排序为止。
Shell排序算法的特点
希尔排序是基于插入排序的以下两点性质而提出改进方法的：
插入排序在对几乎已经排好序的数据操作时， 效率高， 即可以达到线性排序的效率[list][*]但插入排序一般来说是低效的， 因为插入排序每次只能将数据移动一位
[/*]
[/list]
时间复杂度：最坏情况下为O(n^2)，平均时间复杂度为O(nlogn)；
空间复杂度：归并排序需要一个大小为1的临时存储空间用以保存合并序列，所以空间复杂度为O(1)
算法稳定性：从上面图片中可以看出，数字5在排序后交换了位置，所以它是不稳定的算法。
例如：12、5、9、34、6、8、33、56、89、0、7、4、22、55、77
具体步骤：
void Shell(int *arr,int len,int gap)
{
for(int i = gap;i < len;i++)
{
int temp = arr;
int j = 0;
for(j = i-gap;j >= 0;j-=gap)
{
if(arr[j] > temp)
{
arr[j+gap] = arr[j];
}
else
{
break;
}
}
arr[j+gap] = temp;
}
}
void Shell_Sort(int *arr,int len)
{
int drr = {5,3,1}; //drr为分的组数，这里5，3，1不固定，但必须相互为素数，且最后数为1
int lend = sizeof(drr)/sizeof(drr[0]);
for(int i = 0;i < lend;i++)
{
Shell(arr,len,drr);
}
}
引用文章：
https://blog.csdn.net/FDk_LCL/java/article/details/90581904
https://www.cnblogs.com/guopengxia0719/p/10520561.html
https://www.cnblogs.com/BaoZiY/p/10931406.html
查看全部
一、直接插入排序
实例如下所示：
定义的数组 ： {23,34,56,78,65,90,88,92,18,21}
过程如下所示：
【23】 34 56 78 65 90 88 92 18 21
第 1 次排序结果： 【23 34】 56 78 65 90 88 92 18 21
——用34插入到【23】序列中，34>23，故插入后的顺序是【23，34】
第 2 次排序结果： 【 23 34 56 】78 65 90 88 92 18 21
——用56插入到【23，34】序列中，56>34，故插入后的顺序是【23，34，56】
第 3 次排序结果： 【23 34 56 78】65 90 88 92 18 21
——用78插入到【23，34，56】序列中，78>56，故插入后的顺序是【23，34，56，78】
第 4 次排序结果： 【23 34 56 65 78 】90 88 92 18 21
——用65插入到【23，34，56，78】序列中，65<78，所以78后移一位，和56比较，65>56,故插入后的顺序是【23，34，56，65, 78】
第 5 次排序结果： 【23 34 56 65 78 90 】 88 92 18 21
——用90插入到【23，34，56，65, 78】序列中，78<90 ,故插入后的顺序是【23 34 56 65 78 90 】
第 6 次排序结果： 23 34 56 65 78 88 90 92 18 21
——用88插入到【23 34 56 65 78 90 】序列中，90>88 ,所以90后移一位,故插入后的顺序是【23 34 56 65 78 88 90】
第 7 次排序结果： 23 34 56 65 78 88 90 92 18 21
——用92插入到【23 34 56 65 78 90 】序列中，90<92 ,故插入后的顺序是【23 34 56 65 78 90 92 】
第 8 次排序结果： 18 23 34 56 65 78 88 90 92 21
——用18插入到【23 34 56 65 78 90 92 】序列中，18<92，所以92后移一位，和90比较，90>18,依次后移，直到第一位23，因为18<23, 故插入后的顺序是【18 23 34 56 65 78 88 90 92】
第 9 次排序结果： 18 21 23 34 56 65 78 88 90 92
——用21插入到【23 34 56 65 78 90 92 】序列中，21<92，故92后移一位，和90比较，90>21,依次后移，直到第一位18，因为18<21, 故插入后的顺序是【18 21 23 34 56 65 78 88 90 92】
C语言实现：
二、Shell排序：直接插入排序算法的一种高速而稳定的改进版本
希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。
先取一个小于n的整数d1作为第一个增量，把文件的全部记录分组。所有距离为d1的倍数的记录放在同一个组中。先在各组内进行直接插入排序；然后，取第二个增量d2<d1重复上述的分组和排序，直至所取的增量=1(<…<d2<d1)，即所有记录放在同一组中进行直接插入排序为止。
Shell排序算法的特点
例如：12、5、9、34、6、8、33、56、89、0、7、4、22、55、77
具体步骤：
引用文章：
https://blog.csdn.net/FDk_LCL/java/article/details/90581904
https://www.cnblogs.com/guopengxia0719/p/10520561.html
https://www.cnblogs.com/BaoZiY/p/10931406.html
直接插入排序（Straight Insertion Sort）是一种最简单的排序方法，其基本操作是将一条记录插入到已排好的有序表中，从而得到一个新的、记录数量增1的有序表。直接插入排序的时间复杂度为 O(n2)。
实例如下所示：
定义的数组 ： {23,34,56,78,65,90,88,92,18,21}
过程如下所示：
【23】 34 56 78 65 90 88 92 18 21
第 1 次排序结果： 【23 34】 56 78 65 90 88 92 18 21
——用34插入到【23】序列中，34>23，故插入后的顺序是【23，34】
第 2 次排序结果： 【 23 34 56 】78 65 90 88 92 18 21
——用56插入到【23，34】序列中，56>34，故插入后的顺序是【23，34，56】
第 3 次排序结果： 【23 34 56 78】65 90 88 92 18 21
——用78插入到【23，34，56】序列中，78>56，故插入后的顺序是【23，34，56，78】
第 4 次排序结果： 【23 34 56 65 78 】90 88 92 18 21
——用65插入到【23，34，56，78】序列中，65<78，所以78后移一位，和56比较，65>56,故插入后的顺序是【23，34，56，65, 78】
第 5 次排序结果： 【23 34 56 65 78 90 】 88 92 18 21
——用90插入到【23，34，56，65, 78】序列中，78<90 ,故插入后的顺序是【23 34 56 65 78 90 】
第 6 次排序结果： 23 34 56 65 78 88 90 92 18 21
——用88插入到【23 34 56 65 78 90 】序列中，90>88 ,所以90后移一位,故插入后的顺序是【23 34 56 65 78 88 90】
第 7 次排序结果： 23 34 56 65 78 88 90 92 18 21
——用92插入到【23 34 56 65 78 90 】序列中，90<92 ,故插入后的顺序是【23 34 56 65 78 90 92 】
第 8 次排序结果： 18 23 34 56 65 78 88 90 92 21
——用18插入到【23 34 56 65 78 90 92 】序列中，18<92，所以92后移一位，和90比较，90>18,依次后移，直到第一位23，因为18<23, 故插入后的顺序是【18 23 34 56 65 78 88 90 92】
第 9 次排序结果： 18 21 23 34 56 65 78 88 90 92
——用21插入到【23 34 56 65 78 90 92 】序列中，21<92，故92后移一位，和90比较，90>21,依次后移，直到第一位18，因为18<21, 故插入后的顺序是【18 21 23 34 56 65 78 88 90 92】
C语言实现：
#include <stdio.h>
//自定义的输出函数
void print(int a, int n ,int i){
printf("%d:",i);
for(int j=0; j<8; j++){
printf("%d",a[j]);
}
printf("\n");
}
//直接插入排序函数
void InsertSort(int a, int n)
{
for(int i= 1; i<n; i++){
if(a < a[i-1]){//若第 i 个元素大于 i-1 元素则直接插入；反之，需要找到适当的插入位置后在插入。
int j= i-1;
int x = a;
while(j>-1 && x < a[j]){ //采用顺序查找方式找到插入的位置，在查找的同时，将数组中的元素进行后移操作，给插入元素腾出空间
a[j+1] = a[j];
j--;
}
a[j+1] = x; //插入到正确位置
}
print(a,n,i);//打印每次排序后的结果
}
}
int main(){
int a[8] = {3,1,7,5,2,4,9,6};
InsertSort(a,8);
return 0;
}
二、Shell排序：直接插入排序算法的一种高速而稳定的改进版本
希尔排序，也称递减增量排序算法，是一种插入排序算法，它出自D.L.Shell，因此而得名。Shell排序又称作缩小增量排序。Shell排序的执行时间依赖于增量序列。
希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。
先取一个小于n的整数d1作为第一个增量，把文件的全部记录分组。所有距离为d1的倍数的记录放在同一个组中。先在各组内进行直接插入排序；然后，取第二个增量d2<d1重复上述的分组和排序，直至所取的增量=1(<…<d2<d1)，即所有记录放在同一组中进行直接插入排序为止。
Shell排序算法的特点
希尔排序是基于插入排序的以下两点性质而提出改进方法的：
- 插入排序在对几乎已经排好序的数据操作时， 效率高， 即可以达到线性排序的效率[list][*]但插入排序一般来说是低效的， 因为插入排序每次只能将数据移动一位
[/*]
[/list]
时间复杂度：最坏情况下为O(n^2)，平均时间复杂度为O(nlogn)；
空间复杂度：归并排序需要一个大小为1的临时存储空间用以保存合并序列，所以空间复杂度为O(1)
算法稳定性：从上面图片中可以看出，数字5在排序后交换了位置，所以它是不稳定的算法。
例如：12、5、9、34、6、8、33、56、89、0、7、4、22、55、77
具体步骤：
void Shell(int *arr,int len,int gap)
{
for(int i = gap;i < len;i++)
{
int temp = arr;
int j = 0;
for(j = i-gap;j >= 0;j-=gap)
{
if(arr[j] > temp)
{
arr[j+gap] = arr[j];
}
else
{
break;
}
}
arr[j+gap] = temp;
}
}
void Shell_Sort(int *arr,int len)
{
int drr = {5,3,1}; //drr为分的组数，这里5，3，1不固定，但必须相互为素数，且最后数为1
int lend = sizeof(drr)/sizeof(drr[0]);
for(int i = 0;i < lend;i++)
{
Shell(arr,len,drr);
}
}
引用文章：
https://blog.csdn.net/FDk_LCL/java/article/details/90581904
https://www.cnblogs.com/guopengxia0719/p/10520561.html
https://www.cnblogs.com/BaoZiY/p/10931406.html
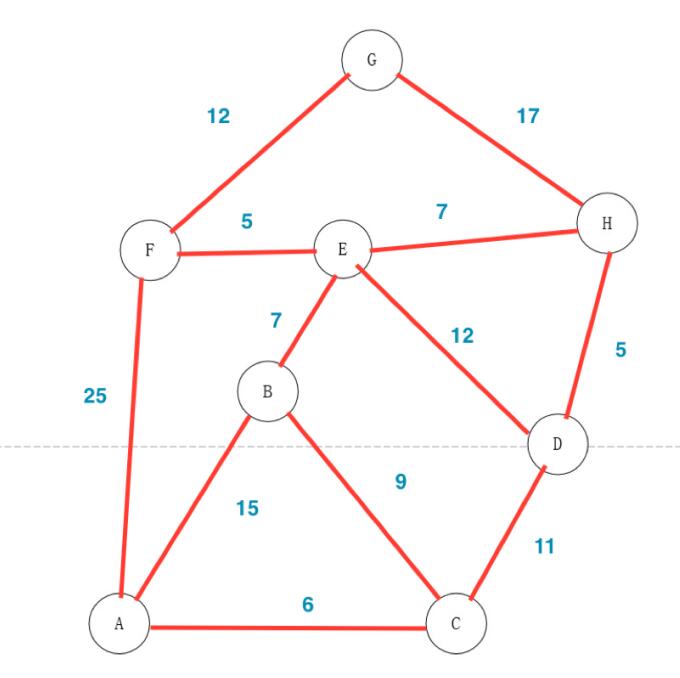
2017自如技术大赛研发组题目七：单源最短路径算法问题
PHP • zkbhj 发表了文章 • 0 个评论 • 1881 次浏览 • 2017-12-04 00:08
7. 自如今年年底就会拥有50W间房子，大家知道每间房房子都是需要配置完才能出租给自如客的，整个房租的配置过程是很复杂的，每天都需要大量的物流师傅将家电，家具等物品从仓库送到需要配置的每个房间。为了能在更多的时间配置更多的房子，我要不断的优化物流从仓库A到房间G的路径或者仓库B到房间E的距离，请写出一种算法给你任意图中两点，计算出两点之间的最短距离。
注：A B C D E F G H 都可能是仓库或者房间，点与点之间是距离
示例：
输入：AE
输出：最短距离：22
【PHP实现】<?php
/**
* Class Road
* 两点间最短路径计算类
* User: 郑凯
* Date: 2017/12/2
* Time: 19:48
* Dijkstra 算法，迪科斯彻算法（Dijkstra），又称为单源最短路径算法。
* Dijstra算法是运用贪心的策略，从源点开始，不断地通过相联通的点找出到其他点的最短距离。
*/
class Road {
//节点对应的字母名
public $pointName = array(
0 => "A",
1 => "B",
2 => "C",
3 => "D",
4 => "E",
5 => "F",
6 => "G",
7 => "H",
);
//地图上的点已经点之间的路径长度
public $points = array(
"A" => array(
"A" => 0,
"B" => 15,
"C" => 6,
"D" => 0,
"E" =>0,
"F" =>25,
"G" =>0,
"H" =>0
),
"B" => array(
"A" => 15,
"B" => 0,
"C" => 9,
"D" => 0,
"E" =>7,
"F" =>0,
"G" =>0,
"H" =>0
),
"C" => array(
"A" => 6,
"B" => 9,
"C" => 0,
"D" => 11,
"E" =>0,
"F" =>0,
"G" =>0,
"H" =>0
),
"D" => array(
"A" => 0,
"B" => 0,
"C" => 11,
"D" => 0,
"E" =>12,
"F" =>0,
"G" =>0,
"H" =>5
),
"E" => array(
"A" => 0,
"B" => 7,
"C" => 0,
"D" => 12,
"E" =>0,
"F" =>5,
"G" =>0,
"H" =>7
),
"F" => array(
"A" => 25,
"B" => 0,
"C" => 0,
"D" => 0,
"E" =>5,
"F" =>0,
"G" =>12,
"H" =>0
),
"G" => array(
"A" => 0,
"B" => 0,
"C" => 0,
"D" => 0,
"E" =>0,
"F" =>12,
"G" =>0,
"H" =>17
),
"H" => array(
"A" => 0,
"B" => 0,
"C" => 0,
"D" => 5,
"E" =>7,
"F" =>0,
"G" =>17,
"H" =>0
),
);
//有向图存储
private $graph = array(
array(0,15,6,0,0,25,0,0),
array(15,0,9,0,7,0,0,0),
array(6,9,0,11,0,0,0,0),
array(0,0,11,0,12,0,0,5),
array(0,7,6,12,0,5,0,7),
array(25,0,6,0,5,0,12,0),
array(0,0,0,0,0,12,0,17),
array(0,0,0,5,7,25,17,0)
);
//设置一个无穷大距离的数字
private $soBig = 999999;
private $path = array();
private function getOptimalPath($a, $b)
{
if($a == $b){
return "start and end could not be one point";
}
//读取已经选择的点
$idx = array_keys($this->points);
$a = array_search($a, $idx);
$b = array_search($b, $idx);
//存储路径上节点距离$a点的最小距离
$c = array();
$path = array();
//初始化距离起点最近的节点的最小距离
for($i=1;$i<8;$i++)
{
if($this->graph[$a][$i]>0)
{
$c[$i] = $this->graph[$a][$i];
$path[$i]['name'] = $this->pointName[$a];
$path[$i]['key'] = $a;
}
else
{
$c[$i] = $this->soBig;
}
}
//用于存储已经选择的节点
$selected = array($a);
$all = array(1,2,3,4,5,6,7);
unset($all[$a-1]);
$others = $all;
// n-1次循环完成转移节点任务
for($i=0;$i<count($this->graph)-1;$i++)
{
//查找剩余节点中距离起点最近的节点v
$current_min = $this->soBig;
$current_min_v = 0;
foreach($others as $k=>$v)
{
if($c[$v] < $current_min)
{
$current_min = $c[$v];
$current_min_v = $v;
}
}
//从$others更新顶点到$selected中
array_push($selected,$current_min_v);
array_splice($others,array_search($current_min_v,$others),1);
//更新最短路径
foreach($others as $k=>$u)
{
if($this->graph[$current_min_v][$u]!=0&&$c[$u]>$c[$current_min_v]+$this->graph[$current_min_v][$u])
{
$path[$u]['name'] = $this->pointName[$current_min_v];
$path[$u]['key'] = $current_min_v;
$c[$u] = $c[$current_min_v]+$this->graph[$current_min_v][$u];
}
}
}
$this->getRoadLine($path,$b,$a);
$finalPath = $this->pointName[$a];
foreach(array_reverse($this->path) as $x => $y){
$finalPath.=$y;
}
$finalPath.=$this->pointName[$b];
return $c[$b]." ".$finalPath;
}
//获取路径信息
public function getRoadLine($path,$b,$a)
{
if($path[$b]['key'] !== $a){
$this->path = $path[$b]['name'];
$this->getRoadLine($path,$path[$b]['key'],$a);
}
}
public function getResult($towPoint){
return $this->getOptimalPath(substr($towPoint,0,1),substr($towPoint, -1));
}
}
//获取输入变量
$params = trim(fgets(STDIN), " \t\n\r\0\x0B");
$road = new Road();
echo $road->getResult($params); 查看全部
注：A B C D E F G H 都可能是仓库或者房间，点与点之间是距离
示例：
输入：AE
输出：最短距离：22
【PHP实现】<?php
/**
* Class Road
* 两点间最短路径计算类
* User: 郑凯
* Date: 2017/12/2
* Time: 19:48
* Dijkstra 算法，迪科斯彻算法（Dijkstra），又称为单源最短路径算法。
* Dijstra算法是运用贪心的策略，从源点开始，不断地通过相联通的点找出到其他点的最短距离。
*/
class Road {
//节点对应的字母名
public $pointName = array(
0 => "A",
1 => "B",
2 => "C",
3 => "D",
4 => "E",
5 => "F",
6 => "G",
7 => "H",
);
//地图上的点已经点之间的路径长度
public $points = array(
"A" => array(
"A" => 0,
"B" => 15,
"C" => 6,
"D" => 0,
"E" =>0,
"F" =>25,
"G" =>0,
"H" =>0
),
"B" => array(
"A" => 15,
"B" => 0,
"C" => 9,
"D" => 0,
"E" =>7,
"F" =>0,
"G" =>0,
"H" =>0
),
"C" => array(
"A" => 6,
"B" => 9,
"C" => 0,
"D" => 11,
"E" =>0,
"F" =>0,
"G" =>0,
"H" =>0
),
"D" => array(
"A" => 0,
"B" => 0,
"C" => 11,
"D" => 0,
"E" =>12,
"F" =>0,
"G" =>0,
"H" =>5
),
"E" => array(
"A" => 0,
"B" => 7,
"C" => 0,
"D" => 12,
"E" =>0,
"F" =>5,
"G" =>0,
"H" =>7
),
"F" => array(
"A" => 25,
"B" => 0,
"C" => 0,
"D" => 0,
"E" =>5,
"F" =>0,
"G" =>12,
"H" =>0
),
"G" => array(
"A" => 0,
"B" => 0,
"C" => 0,
"D" => 0,
"E" =>0,
"F" =>12,
"G" =>0,
"H" =>17
),
"H" => array(
"A" => 0,
"B" => 0,
"C" => 0,
"D" => 5,
"E" =>7,
"F" =>0,
"G" =>17,
"H" =>0
),
);
//有向图存储
private $graph = array(
array(0,15,6,0,0,25,0,0),
array(15,0,9,0,7,0,0,0),
array(6,9,0,11,0,0,0,0),
array(0,0,11,0,12,0,0,5),
array(0,7,6,12,0,5,0,7),
array(25,0,6,0,5,0,12,0),
array(0,0,0,0,0,12,0,17),
array(0,0,0,5,7,25,17,0)
);
//设置一个无穷大距离的数字
private $soBig = 999999;
private $path = array();
private function getOptimalPath($a, $b)
{
if($a == $b){
return "start and end could not be one point";
}
//读取已经选择的点
$idx = array_keys($this->points);
$a = array_search($a, $idx);
$b = array_search($b, $idx);
//存储路径上节点距离$a点的最小距离
$c = array();
$path = array();
//初始化距离起点最近的节点的最小距离
for($i=1;$i<8;$i++)
{
if($this->graph[$a][$i]>0)
{
$c[$i] = $this->graph[$a][$i];
$path[$i]['name'] = $this->pointName[$a];
$path[$i]['key'] = $a;
}
else
{
$c[$i] = $this->soBig;
}
}
//用于存储已经选择的节点
$selected = array($a);
$all = array(1,2,3,4,5,6,7);
unset($all[$a-1]);
$others = $all;
// n-1次循环完成转移节点任务
for($i=0;$i<count($this->graph)-1;$i++)
{
//查找剩余节点中距离起点最近的节点v
$current_min = $this->soBig;
$current_min_v = 0;
foreach($others as $k=>$v)
{
if($c[$v] < $current_min)
{
$current_min = $c[$v];
$current_min_v = $v;
}
}
//从$others更新顶点到$selected中
array_push($selected,$current_min_v);
array_splice($others,array_search($current_min_v,$others),1);
//更新最短路径
foreach($others as $k=>$u)
{
if($this->graph[$current_min_v][$u]!=0&&$c[$u]>$c[$current_min_v]+$this->graph[$current_min_v][$u])
{
$path[$u]['name'] = $this->pointName[$current_min_v];
$path[$u]['key'] = $current_min_v;
$c[$u] = $c[$current_min_v]+$this->graph[$current_min_v][$u];
}
}
}
$this->getRoadLine($path,$b,$a);
$finalPath = $this->pointName[$a];
foreach(array_reverse($this->path) as $x => $y){
$finalPath.=$y;
}
$finalPath.=$this->pointName[$b];
return $c[$b]." ".$finalPath;
}
//获取路径信息
public function getRoadLine($path,$b,$a)
{
if($path[$b]['key'] !== $a){
$this->path = $path[$b]['name'];
$this->getRoadLine($path,$path[$b]['key'],$a);
}
}
public function getResult($towPoint){
return $this->getOptimalPath(substr($towPoint,0,1),substr($towPoint, -1));
}
}
//获取输入变量
$params = trim(fgets(STDIN), " \t\n\r\0\x0B");
$road = new Road();
echo $road->getResult($params); 查看全部
7. 自如今年年底就会拥有50W间房子，大家知道每间房房子都是需要配置完才能出租给自如客的，整个房租的配置过程是很复杂的，每天都需要大量的物流师傅将家电，家具等物品从仓库送到需要配置的每个房间。为了能在更多的时间配置更多的房子，我要不断的优化物流从仓库A到房间G的路径或者仓库B到房间E的距离，请写出一种算法给你任意图中两点，计算出两点之间的最短距离。
注：A B C D E F G H 都可能是仓库或者房间，点与点之间是距离
示例：
输入：AE
输出：最短距离：22
【PHP实现】
注：A B C D E F G H 都可能是仓库或者房间，点与点之间是距离
示例：
输入：AE
输出：最短距离：22
【PHP实现】
<?php
/**
* Class Road
* 两点间最短路径计算类
* User: 郑凯
* Date: 2017/12/2
* Time: 19:48
* Dijkstra 算法，迪科斯彻算法（Dijkstra），又称为单源最短路径算法。
* Dijstra算法是运用贪心的策略，从源点开始，不断地通过相联通的点找出到其他点的最短距离。
*/
class Road {
//节点对应的字母名
public $pointName = array(
0 => "A",
1 => "B",
2 => "C",
3 => "D",
4 => "E",
5 => "F",
6 => "G",
7 => "H",
);
//地图上的点已经点之间的路径长度
public $points = array(
"A" => array(
"A" => 0,
"B" => 15,
"C" => 6,
"D" => 0,
"E" =>0,
"F" =>25,
"G" =>0,
"H" =>0
),
"B" => array(
"A" => 15,
"B" => 0,
"C" => 9,
"D" => 0,
"E" =>7,
"F" =>0,
"G" =>0,
"H" =>0
),
"C" => array(
"A" => 6,
"B" => 9,
"C" => 0,
"D" => 11,
"E" =>0,
"F" =>0,
"G" =>0,
"H" =>0
),
"D" => array(
"A" => 0,
"B" => 0,
"C" => 11,
"D" => 0,
"E" =>12,
"F" =>0,
"G" =>0,
"H" =>5
),
"E" => array(
"A" => 0,
"B" => 7,
"C" => 0,
"D" => 12,
"E" =>0,
"F" =>5,
"G" =>0,
"H" =>7
),
"F" => array(
"A" => 25,
"B" => 0,
"C" => 0,
"D" => 0,
"E" =>5,
"F" =>0,
"G" =>12,
"H" =>0
),
"G" => array(
"A" => 0,
"B" => 0,
"C" => 0,
"D" => 0,
"E" =>0,
"F" =>12,
"G" =>0,
"H" =>17
),
"H" => array(
"A" => 0,
"B" => 0,
"C" => 0,
"D" => 5,
"E" =>7,
"F" =>0,
"G" =>17,
"H" =>0
),
);
//有向图存储
private $graph = array(
array(0,15,6,0,0,25,0,0),
array(15,0,9,0,7,0,0,0),
array(6,9,0,11,0,0,0,0),
array(0,0,11,0,12,0,0,5),
array(0,7,6,12,0,5,0,7),
array(25,0,6,0,5,0,12,0),
array(0,0,0,0,0,12,0,17),
array(0,0,0,5,7,25,17,0)
);
//设置一个无穷大距离的数字
private $soBig = 999999;
private $path = array();
private function getOptimalPath($a, $b)
{
if($a == $b){
return "start and end could not be one point";
}
//读取已经选择的点
$idx = array_keys($this->points);
$a = array_search($a, $idx);
$b = array_search($b, $idx);
//存储路径上节点距离$a点的最小距离
$c = array();
$path = array();
//初始化距离起点最近的节点的最小距离
for($i=1;$i<8;$i++)
{
if($this->graph[$a][$i]>0)
{
$c[$i] = $this->graph[$a][$i];
$path[$i]['name'] = $this->pointName[$a];
$path[$i]['key'] = $a;
}
else
{
$c[$i] = $this->soBig;
}
}
//用于存储已经选择的节点
$selected = array($a);
$all = array(1,2,3,4,5,6,7);
unset($all[$a-1]);
$others = $all;
// n-1次循环完成转移节点任务
for($i=0;$i<count($this->graph)-1;$i++)
{
//查找剩余节点中距离起点最近的节点v
$current_min = $this->soBig;
$current_min_v = 0;
foreach($others as $k=>$v)
{
if($c[$v] < $current_min)
{
$current_min = $c[$v];
$current_min_v = $v;
}
}
//从$others更新顶点到$selected中
array_push($selected,$current_min_v);
array_splice($others,array_search($current_min_v,$others),1);
//更新最短路径
foreach($others as $k=>$u)
{
if($this->graph[$current_min_v][$u]!=0&&$c[$u]>$c[$current_min_v]+$this->graph[$current_min_v][$u])
{
$path[$u]['name'] = $this->pointName[$current_min_v];
$path[$u]['key'] = $current_min_v;
$c[$u] = $c[$current_min_v]+$this->graph[$current_min_v][$u];
}
}
}
$this->getRoadLine($path,$b,$a);
$finalPath = $this->pointName[$a];
foreach(array_reverse($this->path) as $x => $y){
$finalPath.=$y;
}
$finalPath.=$this->pointName[$b];
return $c[$b]." ".$finalPath;
}
//获取路径信息
public function getRoadLine($path,$b,$a)
{
if($path[$b]['key'] !== $a){
$this->path = $path[$b]['name'];
$this->getRoadLine($path,$path[$b]['key'],$a);
}
}
public function getResult($towPoint){
return $this->getOptimalPath(substr($towPoint,0,1),substr($towPoint, -1));
}
}
//获取输入变量
$params = trim(fgets(STDIN), " \t\n\r\0\x0B");
$road = new Road();
echo $road->getResult($params);
2017自如技术大赛研发组题目六：木木熊问题（类约瑟夫环问题）
PHP • zkbhj 发表了文章 • 0 个评论 • 1977 次浏览 • 2017-12-04 00:06
6. 每年夏季自如都会组织夏季夏令营活动，每年组委会都会给来京参加夏令营的小朋友准备好多礼物，今年也是如此。
组委会准备了一些小游戏来获得这些礼物，其中有一个游戏是这样的：组委会让小朋友围成一个圈。然后随机制定一个数e,让编号为0的小朋友开始报数。每次喊道e-1的小朋友直接出列，淘汰出局。从本次喊道e-1的下一个小朋友开始，继续从0报数...e-1淘汰出局...一直这样进行....最后进行到最后一个小朋友，这位小朋友可以拿到“熊帅”亲笔签名的“木木”熊毛绒玩具。
(注：小朋友的编号是从0到n-1)
示例：
输入：n=1314 e=520
输出：796
【PHP实现】
<?php
/**
* Created by PhpStorm.
* User: ZKBHJ
* Date: 2017/12/2
* Time: 18:14
*/
class Summer {
//小朋友总数
public $childCounts = 1314;
//小朋友围成的圈儿
public $childCircle = array();
//指定的随机数
public $e = 520;
//初始化围成一个圈儿
private function initCircle()
{
for($i = 0; $i< $this->childCounts; $i++){
$this->childCircle[$i] = $i;
}
}
private function findChild()
{
$index = 0;
for ($i = 2; $i <= $this->childCounts; $i ++) {
$index = ($index + $this->e) % $i;
}
return $index;
}
public function getResult()
{
$this->initCircle();
return $this->findChild();
}
}
//获取输入变量
$params = explode(' ', trim(fgets(STDIN), " \t\n\r\0\x0B[]"));
foreach($params as $k => $v){
$params[$k] = explode('=',$v);
}
$summer = new Summer();
$summer->childCounts = $params[0][1];
$summer->e = $params[1][1];
echo $summer->getResult(); 查看全部
组委会准备了一些小游戏来获得这些礼物，其中有一个游戏是这样的：组委会让小朋友围成一个圈。然后随机制定一个数e,让编号为0的小朋友开始报数。每次喊道e-1的小朋友直接出列，淘汰出局。从本次喊道e-1的下一个小朋友开始，继续从0报数...e-1淘汰出局...一直这样进行....最后进行到最后一个小朋友，这位小朋友可以拿到“熊帅”亲笔签名的“木木”熊毛绒玩具。
(注：小朋友的编号是从0到n-1)
示例：
输入：n=1314 e=520
输出：796
【PHP实现】
<?php
/**
* Created by PhpStorm.
* User: ZKBHJ
* Date: 2017/12/2
* Time: 18:14
*/
class Summer {
//小朋友总数
public $childCounts = 1314;
//小朋友围成的圈儿
public $childCircle = array();
//指定的随机数
public $e = 520;
//初始化围成一个圈儿
private function initCircle()
{
for($i = 0; $i< $this->childCounts; $i++){
$this->childCircle[$i] = $i;
}
}
private function findChild()
{
$index = 0;
for ($i = 2; $i <= $this->childCounts; $i ++) {
$index = ($index + $this->e) % $i;
}
return $index;
}
public function getResult()
{
$this->initCircle();
return $this->findChild();
}
}
//获取输入变量
$params = explode(' ', trim(fgets(STDIN), " \t\n\r\0\x0B[]"));
foreach($params as $k => $v){
$params[$k] = explode('=',$v);
}
$summer = new Summer();
$summer->childCounts = $params[0][1];
$summer->e = $params[1][1];
echo $summer->getResult(); 查看全部
6. 每年夏季自如都会组织夏季夏令营活动，每年组委会都会给来京参加夏令营的小朋友准备好多礼物，今年也是如此。
组委会准备了一些小游戏来获得这些礼物，其中有一个游戏是这样的：组委会让小朋友围成一个圈。然后随机制定一个数e,让编号为0的小朋友开始报数。每次喊道e-1的小朋友直接出列，淘汰出局。从本次喊道e-1的下一个小朋友开始，继续从0报数...e-1淘汰出局...一直这样进行....最后进行到最后一个小朋友，这位小朋友可以拿到“熊帅”亲笔签名的“木木”熊毛绒玩具。
(注：小朋友的编号是从0到n-1)
示例：
输入：n=1314 e=520
输出：796
【PHP实现】
组委会准备了一些小游戏来获得这些礼物，其中有一个游戏是这样的：组委会让小朋友围成一个圈。然后随机制定一个数e,让编号为0的小朋友开始报数。每次喊道e-1的小朋友直接出列，淘汰出局。从本次喊道e-1的下一个小朋友开始，继续从0报数...e-1淘汰出局...一直这样进行....最后进行到最后一个小朋友，这位小朋友可以拿到“熊帅”亲笔签名的“木木”熊毛绒玩具。
(注：小朋友的编号是从0到n-1)
示例：
输入：n=1314 e=520
输出：796
【PHP实现】
<?php
/**
* Created by PhpStorm.
* User: ZKBHJ
* Date: 2017/12/2
* Time: 18:14
*/
class Summer {
//小朋友总数
public $childCounts = 1314;
//小朋友围成的圈儿
public $childCircle = array();
//指定的随机数
public $e = 520;
//初始化围成一个圈儿
private function initCircle()
{
for($i = 0; $i< $this->childCounts; $i++){
$this->childCircle[$i] = $i;
}
}
private function findChild()
{
$index = 0;
for ($i = 2; $i <= $this->childCounts; $i ++) {
$index = ($index + $this->e) % $i;
}
return $index;
}
public function getResult()
{
$this->initCircle();
return $this->findChild();
}
}
//获取输入变量
$params = explode(' ', trim(fgets(STDIN), " \t\n\r\0\x0B[]"));
foreach($params as $k => $v){
$params[$k] = explode('=',$v);
}
$summer = new Summer();
$summer->childCounts = $params[0][1];
$summer->e = $params[1][1];
echo $summer->getResult();
2017自如技术大赛研发组题目五：订单最优分配问题
PHP • zkbhj 发表了文章 • 0 个评论 • 1494 次浏览 • 2017-12-04 00:04
5. 服务目前每月会对搬家师傅进行评级，根据师傅的评级排名结果，我们将优先保证最优师傅的全天订单
假设师傅每天工作8个小时，给定一天n个订单，每个订单其占用时间长为Ti,挣取价值为Vi,1
现请您为师傅安排订单，并保证师傅挣取价值最大
输入格式
输入n组数据，每组以逗号分隔并且每一个订单的编号，时长，挣取价值，数字以空格分隔
输出格式
输出争取价值，订单编号，订单编号按照价值由大到小排序，争取价值相同，则按照每小时平均争取价值由大到小排序
输入样例
[MV10001 2 100,MV10002 3 120,MV10003 1 200,MV10004 3 200,MV10005 4 70,MV10006 3 120,MV10007 2 10,MV10008 2 30,MV10009 6 500,MV10010 3 400]
输出样例
800 MV10010 MV10003 MV10004
【PHP实现】
<?php
/**
* Class ServiceOrder
* 服务师傅订单最优分配计算
* User: 郑凯
* Date: 2017/12/2
* Time: 18:13
*/
class ServiceOrder {
//待分配的订单数组
public $orderList = array();
//服务师傅每天的工作时长
public $workTime = 8;
//最终筛选出来的收益最大订单列表
public $finalOrderList = array();
//按照预设好的格式，将数据进行初始化，装填到数组中
public function initOrder($orderList)
{
//去除前后多余的[]
$orderList = substr($orderList, 1);
$orderList = substr($orderList, 0, -1);
$tempArray = explode(",",$orderList);
foreach($tempArray as $key => $value){
$this->orderList[$key] = explode(" ",$value);
}
}
function arraySequence($array, $field, $sort = 'SORT_DESC')
{
$arrSort = array();
foreach ($array as $uniqid => $row) {
foreach ($row as $key => $value) {
$arrSort[$key][$uniqid] = $value;
}
}
array_multisort($arrSort[$field], constant($sort), $array);
return $array;
}
//给师傅按最大收益安排订单
public function planOrder()
{
//计算每个订单的平均赚取收益
foreach($this->orderList as $key => $value){
$this->orderList[$key][3] = $value[2]/$value[1];
}
//将订单按照平均赚取收益由高到低排序
$this->orderList = $this->arraySequence($this->orderList,'3','SORT_DESC');
//按照每日工作时长限制，取收益率最高的头几个订单
$workTime = 0;
foreach($this->orderList as $k => $v){
if($this->workTime - $workTime >= $v[1]){
$this->finalOrderList[] = $v;
$workTime+=$v[1];
}
}
}
public function printOrder()
{
//输出总收益
$string = array_sum(array_map(create_function('$val', 'return $val["2"];'), $this->finalOrderList))." ";
//输出订单编号（按单笔订单收益由高到低排序，相同的，则按照平均赚取收益由高到低排序）
foreach($this->finalOrderList as $k => $v){
$total[$k] = $v[2];
$average[$k] = $v[3];
}
array_multisort($total, SORT_DESC, $average, SORT_DESC, $this->finalOrderList);
//输出订单号
foreach($this->finalOrderList as $k => $v){
$string .= $v[0]." ";
}
return $string;
}
public function getResult()
{
$this->planOrder();
return $this->printOrder();
}
}
//获取输入变量
$orderList = trim(fgets(STDIN), " \t\n\r\0\x0B");
$service = new ServiceOrder();
$service->initOrder($orderList);
echo $service->getResult(); 查看全部
假设师傅每天工作8个小时，给定一天n个订单，每个订单其占用时间长为Ti,挣取价值为Vi,1
现请您为师傅安排订单，并保证师傅挣取价值最大
输入格式
输入n组数据，每组以逗号分隔并且每一个订单的编号，时长，挣取价值，数字以空格分隔
输出格式
输出争取价值，订单编号，订单编号按照价值由大到小排序，争取价值相同，则按照每小时平均争取价值由大到小排序
输入样例
[MV10001 2 100,MV10002 3 120,MV10003 1 200,MV10004 3 200,MV10005 4 70,MV10006 3 120,MV10007 2 10,MV10008 2 30,MV10009 6 500,MV10010 3 400]
输出样例
800 MV10010 MV10003 MV10004
【PHP实现】
<?php
/**
* Class ServiceOrder
* 服务师傅订单最优分配计算
* User: 郑凯
* Date: 2017/12/2
* Time: 18:13
*/
class ServiceOrder {
//待分配的订单数组
public $orderList = array();
//服务师傅每天的工作时长
public $workTime = 8;
//最终筛选出来的收益最大订单列表
public $finalOrderList = array();
//按照预设好的格式，将数据进行初始化，装填到数组中
public function initOrder($orderList)
{
//去除前后多余的[]
$orderList = substr($orderList, 1);
$orderList = substr($orderList, 0, -1);
$tempArray = explode(",",$orderList);
foreach($tempArray as $key => $value){
$this->orderList[$key] = explode(" ",$value);
}
}
function arraySequence($array, $field, $sort = 'SORT_DESC')
{
$arrSort = array();
foreach ($array as $uniqid => $row) {
foreach ($row as $key => $value) {
$arrSort[$key][$uniqid] = $value;
}
}
array_multisort($arrSort[$field], constant($sort), $array);
return $array;
}
//给师傅按最大收益安排订单
public function planOrder()
{
//计算每个订单的平均赚取收益
foreach($this->orderList as $key => $value){
$this->orderList[$key][3] = $value[2]/$value[1];
}
//将订单按照平均赚取收益由高到低排序
$this->orderList = $this->arraySequence($this->orderList,'3','SORT_DESC');
//按照每日工作时长限制，取收益率最高的头几个订单
$workTime = 0;
foreach($this->orderList as $k => $v){
if($this->workTime - $workTime >= $v[1]){
$this->finalOrderList[] = $v;
$workTime+=$v[1];
}
}
}
public function printOrder()
{
//输出总收益
$string = array_sum(array_map(create_function('$val', 'return $val["2"];'), $this->finalOrderList))." ";
//输出订单编号（按单笔订单收益由高到低排序，相同的，则按照平均赚取收益由高到低排序）
foreach($this->finalOrderList as $k => $v){
$total[$k] = $v[2];
$average[$k] = $v[3];
}
array_multisort($total, SORT_DESC, $average, SORT_DESC, $this->finalOrderList);
//输出订单号
foreach($this->finalOrderList as $k => $v){
$string .= $v[0]." ";
}
return $string;
}
public function getResult()
{
$this->planOrder();
return $this->printOrder();
}
}
//获取输入变量
$orderList = trim(fgets(STDIN), " \t\n\r\0\x0B");
$service = new ServiceOrder();
$service->initOrder($orderList);
echo $service->getResult(); 查看全部
5. 服务目前每月会对搬家师傅进行评级，根据师傅的评级排名结果，我们将优先保证最优师傅的全天订单
假设师傅每天工作8个小时，给定一天n个订单，每个订单其占用时间长为Ti,挣取价值为Vi,1
现请您为师傅安排订单，并保证师傅挣取价值最大
输入格式
输入n组数据，每组以逗号分隔并且每一个订单的编号，时长，挣取价值，数字以空格分隔
输出格式
输出争取价值，订单编号，订单编号按照价值由大到小排序，争取价值相同，则按照每小时平均争取价值由大到小排序
输入样例
[MV10001 2 100,MV10002 3 120,MV10003 1 200,MV10004 3 200,MV10005 4 70,MV10006 3 120,MV10007 2 10,MV10008 2 30,MV10009 6 500,MV10010 3 400]
输出样例
800 MV10010 MV10003 MV10004
【PHP实现】
假设师傅每天工作8个小时，给定一天n个订单，每个订单其占用时间长为Ti,挣取价值为Vi,1
现请您为师傅安排订单，并保证师傅挣取价值最大
输入格式
输入n组数据，每组以逗号分隔并且每一个订单的编号，时长，挣取价值，数字以空格分隔
输出格式
输出争取价值，订单编号，订单编号按照价值由大到小排序，争取价值相同，则按照每小时平均争取价值由大到小排序
输入样例
[MV10001 2 100,MV10002 3 120,MV10003 1 200,MV10004 3 200,MV10005 4 70,MV10006 3 120,MV10007 2 10,MV10008 2 30,MV10009 6 500,MV10010 3 400]
输出样例
800 MV10010 MV10003 MV10004
【PHP实现】
<?php
/**
* Class ServiceOrder
* 服务师傅订单最优分配计算
* User: 郑凯
* Date: 2017/12/2
* Time: 18:13
*/
class ServiceOrder {
//待分配的订单数组
public $orderList = array();
//服务师傅每天的工作时长
public $workTime = 8;
//最终筛选出来的收益最大订单列表
public $finalOrderList = array();
//按照预设好的格式，将数据进行初始化，装填到数组中
public function initOrder($orderList)
{
//去除前后多余的[]
$orderList = substr($orderList, 1);
$orderList = substr($orderList, 0, -1);
$tempArray = explode(",",$orderList);
foreach($tempArray as $key => $value){
$this->orderList[$key] = explode(" ",$value);
}
}
function arraySequence($array, $field, $sort = 'SORT_DESC')
{
$arrSort = array();
foreach ($array as $uniqid => $row) {
foreach ($row as $key => $value) {
$arrSort[$key][$uniqid] = $value;
}
}
array_multisort($arrSort[$field], constant($sort), $array);
return $array;
}
//给师傅按最大收益安排订单
public function planOrder()
{
//计算每个订单的平均赚取收益
foreach($this->orderList as $key => $value){
$this->orderList[$key][3] = $value[2]/$value[1];
}
//将订单按照平均赚取收益由高到低排序
$this->orderList = $this->arraySequence($this->orderList,'3','SORT_DESC');
//按照每日工作时长限制，取收益率最高的头几个订单
$workTime = 0;
foreach($this->orderList as $k => $v){
if($this->workTime - $workTime >= $v[1]){
$this->finalOrderList[] = $v;
$workTime+=$v[1];
}
}
}
public function printOrder()
{
//输出总收益
$string = array_sum(array_map(create_function('$val', 'return $val["2"];'), $this->finalOrderList))." ";
//输出订单编号（按单笔订单收益由高到低排序，相同的，则按照平均赚取收益由高到低排序）
foreach($this->finalOrderList as $k => $v){
$total[$k] = $v[2];
$average[$k] = $v[3];
}
array_multisort($total, SORT_DESC, $average, SORT_DESC, $this->finalOrderList);
//输出订单号
foreach($this->finalOrderList as $k => $v){
$string .= $v[0]." ";
}
return $string;
}
public function getResult()
{
$this->planOrder();
return $this->printOrder();
}
}
//获取输入变量
$orderList = trim(fgets(STDIN), " \t\n\r\0\x0B");
$service = new ServiceOrder();
$service->initOrder($orderList);
echo $service->getResult();
2017自如技术大赛研发组题目四：蓄水池蓄水量计算问题
PHP • zkbhj 发表了文章 • 0 个评论 • 2025 次浏览 • 2017-12-04 00:02
4. 自如寓打算门口用砖头围立一个蓄水池子，从上面看凹凸不平，凹的地方会有积水。那如果用数字代表每个砖头的高度，就形成一个二维数据（如示例），请问这个池子能存储多少单位的水？
例如二维数组为：
9 9 9 9<br>
3 0 0 9<br>
7 8 9 6<br>
时，答案是中间的0,0位置可以存储3（因为其外面最低是3）个单位的水，因此答案为3+3=6
示例：
输入：[1 1 1 1,1 0 0 1,1 1 1 1]
输出：2
【PHP实现】<?php
/**
* Class Pool
* 蓄水池蓄水量计算类
* User: 郑凯
* Date: 2017/12/2
* Time: 15:35
*/
class WaterPool {
//水池数组(二维数组)
public $poolArray = array();
//水池中凹的地方的数量
public $aoCounts = 0;
//水池中木桶效应的最低“短板”数量（决定单个凹的地方的储水量）
public $bottomCounts = 0;
private function getWater()
{
//遍历水池数组(二维数组)
$bottomTemp = array("height"=>9,"counts"=>0);
foreach($this->poolArray as $key => $value){
foreach($value as $k => $v){
//统计水池中凹的地方的数量
if($v == 0){
$this->aoCounts++;
}
//统计水池中木桶效应的最低“短板”数量
if($bottomTemp["height"] > $v && $v != 0){
$bottomTemp["height"] = $v;
$bottomTemp["counts"] = 1;
}elseif($bottomTemp["height"] == $v){
$bottomTemp["counts"]++;
}
}
}
//计算水池中的最多储水量
return $this->aoCounts * $bottomTemp["height"];
}
//得到结果
public function getResult()
{
return $this->getWater();
}
}
//获取输入变量
$params = explode(',', trim(fgets(STDIN), " \t\n\r\0\x0B"));
foreach($params as $k => $v){
$params[$k] = explode(' ',$v);
}
//实例化
$pool = new WaterPool();
$pool->poolArray = $params;
echo $pool->getResult(); 查看全部
例如二维数组为：
9 9 9 9<br>
3 0 0 9<br>
7 8 9 6<br>
时，答案是中间的0,0位置可以存储3（因为其外面最低是3）个单位的水，因此答案为3+3=6
示例：
输入：[1 1 1 1,1 0 0 1,1 1 1 1]
输出：2
【PHP实现】<?php
/**
* Class Pool
* 蓄水池蓄水量计算类
* User: 郑凯
* Date: 2017/12/2
* Time: 15:35
*/
class WaterPool {
//水池数组(二维数组)
public $poolArray = array();
//水池中凹的地方的数量
public $aoCounts = 0;
//水池中木桶效应的最低“短板”数量（决定单个凹的地方的储水量）
public $bottomCounts = 0;
private function getWater()
{
//遍历水池数组(二维数组)
$bottomTemp = array("height"=>9,"counts"=>0);
foreach($this->poolArray as $key => $value){
foreach($value as $k => $v){
//统计水池中凹的地方的数量
if($v == 0){
$this->aoCounts++;
}
//统计水池中木桶效应的最低“短板”数量
if($bottomTemp["height"] > $v && $v != 0){
$bottomTemp["height"] = $v;
$bottomTemp["counts"] = 1;
}elseif($bottomTemp["height"] == $v){
$bottomTemp["counts"]++;
}
}
}
//计算水池中的最多储水量
return $this->aoCounts * $bottomTemp["height"];
}
//得到结果
public function getResult()
{
return $this->getWater();
}
}
//获取输入变量
$params = explode(',', trim(fgets(STDIN), " \t\n\r\0\x0B"));
foreach($params as $k => $v){
$params[$k] = explode(' ',$v);
}
//实例化
$pool = new WaterPool();
$pool->poolArray = $params;
echo $pool->getResult(); 查看全部
4. 自如寓打算门口用砖头围立一个蓄水池子，从上面看凹凸不平，凹的地方会有积水。那如果用数字代表每个砖头的高度，就形成一个二维数据（如示例），请问这个池子能存储多少单位的水？
例如二维数组为：
9 9 9 9<br>
3 0 0 9<br>
7 8 9 6<br>
时，答案是中间的0,0位置可以存储3（因为其外面最低是3）个单位的水，因此答案为3+3=6
示例：
输入：[1 1 1 1,1 0 0 1,1 1 1 1]
输出：2
【PHP实现】
例如二维数组为：
9 9 9 9<br>
3 0 0 9<br>
7 8 9 6<br>
时，答案是中间的0,0位置可以存储3（因为其外面最低是3）个单位的水，因此答案为3+3=6
示例：
输入：[1 1 1 1,1 0 0 1,1 1 1 1]
输出：2
【PHP实现】
<?php
/**
* Class Pool
* 蓄水池蓄水量计算类
* User: 郑凯
* Date: 2017/12/2
* Time: 15:35
*/
class WaterPool {
//水池数组(二维数组)
public $poolArray = array();
//水池中凹的地方的数量
public $aoCounts = 0;
//水池中木桶效应的最低“短板”数量（决定单个凹的地方的储水量）
public $bottomCounts = 0;
private function getWater()
{
//遍历水池数组(二维数组)
$bottomTemp = array("height"=>9,"counts"=>0);
foreach($this->poolArray as $key => $value){
foreach($value as $k => $v){
//统计水池中凹的地方的数量
if($v == 0){
$this->aoCounts++;
}
//统计水池中木桶效应的最低“短板”数量
if($bottomTemp["height"] > $v && $v != 0){
$bottomTemp["height"] = $v;
$bottomTemp["counts"] = 1;
}elseif($bottomTemp["height"] == $v){
$bottomTemp["counts"]++;
}
}
}
//计算水池中的最多储水量
return $this->aoCounts * $bottomTemp["height"];
}
//得到结果
public function getResult()
{
return $this->getWater();
}
}
//获取输入变量
$params = explode(',', trim(fgets(STDIN), " \t\n\r\0\x0B"));
foreach($params as $k => $v){
$params[$k] = explode(' ',$v);
}
//实例化
$pool = new WaterPool();
$pool->poolArray = $params;
echo $pool->getResult();
2017自如技术大赛研发组题目三：给定数字连接最大数
PHP • zkbhj 发表了文章 • 0 个评论 • 1582 次浏览 • 2017-12-04 00:01
3. 给定一个数组，将数组中的数字连接起来，求最大数。
示例：
输入：4,94,9,14,1
输出：9944141
【PHP实现】
<?php
/**
* Class Max
* 计算最大数字
* User: 郑凯
* Date: 2017/12/2
* Time: 14:02
*/
class Max {
//要进行处理的原始数字数组
public $numbers = array();
//经过处理后排序好的数字数组
public $lastNumber = array();
/**
* 获取整数某个位置的数字值
* @param $number
* @param int $position
* @return bool
*/
public function getPositionNumber($number,$position = 0)
{
//将数字当成字符串，将数字分离个位数存到数组中
for($i=0;$i<strlen($number);$i++){
$array[] = substr($number,$i,1);
}
return isset($array[$position])?$array[$position]:false;
}
/**
* 比较两个数，决定谁优先排在前面（即下面注释中的“最大数”）
* @param $a
* @param $b
* @return null
*/
private function compare($a,$b){
//默认最大值是null
$max = null;
//按两个数中数学概念中的最小数的长度进行从高到低每一位数字的对比
for($i = 0; $i<min(array(strlen($a),strlen($b))); $i++){
//如果同一位上的两个数字相等，则继续向下一位比较
if($this->getPositionNumber($a, $i) == $this->getPositionNumber($b, $i)){
continue;
}else{
//如果两个数字不等，则“最大数”是比较大的那个整数，跳出循环，不再继续比较
$this->getPositionNumber($a, $i) > $this->getPositionNumber($b, $i) ? $max = $a:$max = $b;
break;
}
}
//如果走到这里，说明数学概念中最小数的长度的头几位两个整数一样，那么就需要比较较长数字的下一位和较短数字的第一位
//首先判断这两个整数中哪个是短的
//如果两个整数长度一致，说明两个整数一样，则返回谁都可以
//如果较长数字的下一位比较短整数的第一位大，则“最大数”应该是前者，否则，应该是后者
if($max == null){
if(strlen($a)<strlen($b)){
$this->getPositionNumber($b, $i) > $this->getPositionNumber($a,0) ? $max = $b:$max = $a;
}elseif(strlen($a)>strlen($b)){
$this->getPositionNumber($a, $i) > $this->getPositionNumber($b,0) ? $max = $a:$max = $b;
}else{
$max = $a;
}
}
//返回“最大数”
return $max;
}
//主体函数，获取最大数字
public function getMaxNumber()
{
//初始化最大数，赋值为给定数字数组中的第一个
$max = array("key"=> 0, "value"=>$this->numbers[0]);
//对数组中的每个数字进行循环，将其与Max中的数字进行比较
for($j=0 ;$j < count($this->numbers); $j++){
$tempMax = $this->compare($this->numbers[$j],$max['value']);
//如果得到的“最大数”应不是原来的“最大数”，那么进行最大数的更新（更新key和value），这里的key主要用于下面的unset
if($tempMax != $max['value']){
$max['value'] = $tempMax;
$max['key'] = $j;
}
}
//把这一轮比较中的“最大数”放入数组中
$this->lastNumber[] = $max;
//将这个比较出来的“最大数”从原始数组中删除，不再让他捣乱啦
unset($this->numbers[$max['key']]);
//将原始数组重建key
$this->numbers = array_values($this->numbers);
//如果原始数组中还有数组，继续递归调用
if(count($this->numbers) > 0){
$this->getMaxNumber();
}
}
//输出最后连起来最大的数字
public function getResult()
{
$this->getMaxNumber();
foreach($this->lastNumber as $key => $value){
echo $value['value'];
}
}
}
//获取输入变量
$numbers = explode(',', trim(fgets(STDIN), " \t\n\r\0\x0B[]"));
//实例化
$max = new Max();
$max->numbers = $numbers;
$max->getResult(); 查看全部
示例：
输入：4,94,9,14,1
输出：9944141
【PHP实现】
<?php
/**
* Class Max
* 计算最大数字
* User: 郑凯
* Date: 2017/12/2
* Time: 14:02
*/
class Max {
//要进行处理的原始数字数组
public $numbers = array();
//经过处理后排序好的数字数组
public $lastNumber = array();
/**
* 获取整数某个位置的数字值
* @param $number
* @param int $position
* @return bool
*/
public function getPositionNumber($number,$position = 0)
{
//将数字当成字符串，将数字分离个位数存到数组中
for($i=0;$i<strlen($number);$i++){
$array[] = substr($number,$i,1);
}
return isset($array[$position])?$array[$position]:false;
}
/**
* 比较两个数，决定谁优先排在前面（即下面注释中的“最大数”）
* @param $a
* @param $b
* @return null
*/
private function compare($a,$b){
//默认最大值是null
$max = null;
//按两个数中数学概念中的最小数的长度进行从高到低每一位数字的对比
for($i = 0; $i<min(array(strlen($a),strlen($b))); $i++){
//如果同一位上的两个数字相等，则继续向下一位比较
if($this->getPositionNumber($a, $i) == $this->getPositionNumber($b, $i)){
continue;
}else{
//如果两个数字不等，则“最大数”是比较大的那个整数，跳出循环，不再继续比较
$this->getPositionNumber($a, $i) > $this->getPositionNumber($b, $i) ? $max = $a:$max = $b;
break;
}
}
//如果走到这里，说明数学概念中最小数的长度的头几位两个整数一样，那么就需要比较较长数字的下一位和较短数字的第一位
//首先判断这两个整数中哪个是短的
//如果两个整数长度一致，说明两个整数一样，则返回谁都可以
//如果较长数字的下一位比较短整数的第一位大，则“最大数”应该是前者，否则，应该是后者
if($max == null){
if(strlen($a)<strlen($b)){
$this->getPositionNumber($b, $i) > $this->getPositionNumber($a,0) ? $max = $b:$max = $a;
}elseif(strlen($a)>strlen($b)){
$this->getPositionNumber($a, $i) > $this->getPositionNumber($b,0) ? $max = $a:$max = $b;
}else{
$max = $a;
}
}
//返回“最大数”
return $max;
}
//主体函数，获取最大数字
public function getMaxNumber()
{
//初始化最大数，赋值为给定数字数组中的第一个
$max = array("key"=> 0, "value"=>$this->numbers[0]);
//对数组中的每个数字进行循环，将其与Max中的数字进行比较
for($j=0 ;$j < count($this->numbers); $j++){
$tempMax = $this->compare($this->numbers[$j],$max['value']);
//如果得到的“最大数”应不是原来的“最大数”，那么进行最大数的更新（更新key和value），这里的key主要用于下面的unset
if($tempMax != $max['value']){
$max['value'] = $tempMax;
$max['key'] = $j;
}
}
//把这一轮比较中的“最大数”放入数组中
$this->lastNumber[] = $max;
//将这个比较出来的“最大数”从原始数组中删除，不再让他捣乱啦
unset($this->numbers[$max['key']]);
//将原始数组重建key
$this->numbers = array_values($this->numbers);
//如果原始数组中还有数组，继续递归调用
if(count($this->numbers) > 0){
$this->getMaxNumber();
}
}
//输出最后连起来最大的数字
public function getResult()
{
$this->getMaxNumber();
foreach($this->lastNumber as $key => $value){
echo $value['value'];
}
}
}
//获取输入变量
$numbers = explode(',', trim(fgets(STDIN), " \t\n\r\0\x0B[]"));
//实例化
$max = new Max();
$max->numbers = $numbers;
$max->getResult(); 查看全部
3. 给定一个数组，将数组中的数字连接起来，求最大数。
示例：
输入：4,94,9,14,1
输出：9944141
【PHP实现】
示例：
输入：4,94,9,14,1
输出：9944141
【PHP实现】
<?php
/**
* Class Max
* 计算最大数字
* User: 郑凯
* Date: 2017/12/2
* Time: 14:02
*/
class Max {
//要进行处理的原始数字数组
public $numbers = array();
//经过处理后排序好的数字数组
public $lastNumber = array();
/**
* 获取整数某个位置的数字值
* @param $number
* @param int $position
* @return bool
*/
public function getPositionNumber($number,$position = 0)
{
//将数字当成字符串，将数字分离个位数存到数组中
for($i=0;$i<strlen($number);$i++){
$array[] = substr($number,$i,1);
}
return isset($array[$position])?$array[$position]:false;
}
/**
* 比较两个数，决定谁优先排在前面（即下面注释中的“最大数”）
* @param $a
* @param $b
* @return null
*/
private function compare($a,$b){
//默认最大值是null
$max = null;
//按两个数中数学概念中的最小数的长度进行从高到低每一位数字的对比
for($i = 0; $i<min(array(strlen($a),strlen($b))); $i++){
//如果同一位上的两个数字相等，则继续向下一位比较
if($this->getPositionNumber($a, $i) == $this->getPositionNumber($b, $i)){
continue;
}else{
//如果两个数字不等，则“最大数”是比较大的那个整数，跳出循环，不再继续比较
$this->getPositionNumber($a, $i) > $this->getPositionNumber($b, $i) ? $max = $a:$max = $b;
break;
}
}
//如果走到这里，说明数学概念中最小数的长度的头几位两个整数一样，那么就需要比较较长数字的下一位和较短数字的第一位
//首先判断这两个整数中哪个是短的
//如果两个整数长度一致，说明两个整数一样，则返回谁都可以
//如果较长数字的下一位比较短整数的第一位大，则“最大数”应该是前者，否则，应该是后者
if($max == null){
if(strlen($a)<strlen($b)){
$this->getPositionNumber($b, $i) > $this->getPositionNumber($a,0) ? $max = $b:$max = $a;
}elseif(strlen($a)>strlen($b)){
$this->getPositionNumber($a, $i) > $this->getPositionNumber($b,0) ? $max = $a:$max = $b;
}else{
$max = $a;
}
}
//返回“最大数”
return $max;
}
//主体函数，获取最大数字
public function getMaxNumber()
{
//初始化最大数，赋值为给定数字数组中的第一个
$max = array("key"=> 0, "value"=>$this->numbers[0]);
//对数组中的每个数字进行循环，将其与Max中的数字进行比较
for($j=0 ;$j < count($this->numbers); $j++){
$tempMax = $this->compare($this->numbers[$j],$max['value']);
//如果得到的“最大数”应不是原来的“最大数”，那么进行最大数的更新（更新key和value），这里的key主要用于下面的unset
if($tempMax != $max['value']){
$max['value'] = $tempMax;
$max['key'] = $j;
}
}
//把这一轮比较中的“最大数”放入数组中
$this->lastNumber[] = $max;
//将这个比较出来的“最大数”从原始数组中删除，不再让他捣乱啦
unset($this->numbers[$max['key']]);
//将原始数组重建key
$this->numbers = array_values($this->numbers);
//如果原始数组中还有数组，继续递归调用
if(count($this->numbers) > 0){
$this->getMaxNumber();
}
}
//输出最后连起来最大的数字
public function getResult()
{
$this->getMaxNumber();
foreach($this->lastNumber as $key => $value){
echo $value['value'];
}
}
}
//获取输入变量
$numbers = explode(',', trim(fgets(STDIN), " \t\n\r\0\x0B[]"));
//实例化
$max = new Max();
$max->numbers = $numbers;
$max->getResult();
2017自如技术大赛研发组题目二：110的算式计算
PHP • zkbhj 发表了文章 • 0 个评论 • 1426 次浏览 • 2017-12-04 00:00
2. 2016年自如将品质管理中心升级为安全与品质管理中心，并开通了自如举报邮箱。请看下边的算式
1 2 3 4 5 6 7 8 9 = ？（举报邮箱前缀数字）;（备注110）
为了使等式成立，需要在数字间填入加号或者减号（可以不填，但不能填入其它符号）。之间没有填入符号的数字组合成一个数，例如：12+34+56+7-8+9 就是一种合格的填法。
请大家帮忙计算出多少个可能组合吧，至少3个以上算有效
示例
输入：[1 2 3 4 5 6 7 8 9 ]
输出：12+34+56+7-8+9
…………………………
【PHP实现】
<?php
class Fire {
private $numberItems = array();
//用于存储所有可能的情况
private $situation = array();
//设计的最终结果
private $result = 110;
//用于存储计算结果和设计结果一直的情况
private $rightSituation = array();
//用0,1,2分别代表空格、加号和减号
private $symbol = array(0=>"",1=>"+",2=>"-");
private $temp = array();
//获取所有可能出现的情况
public function getSituation($index)
{
if ($index == 8) {
$this->situation[] = $this->temp;
return;
}
//每个空有三种可能，0,1,2
for ($i = 0; $i < 3; $i++) {
$this->temp[$index] = $i;
$this->getSituation($index + 1);
$this->temp[$index] = 0; //恢复原来的状态
}
}
//获得表达式和输出结果
public function calculate()
{
foreach($this->situation as $k => $v){
$number = 1;
$expression = 1;
foreach($v as $key => $value){
switch($value)
{
//空格
case 0:
{
$expression = $expression.$this->numberItems[$key+1];
break;
}
//加号
case 1:
{
$expression = $expression . "+" .$this->numberItems[$key+1];
break;
}
//减号
case 2:
{
$expression = $expression . "-" .$this->numberItems[$key+1];
break;
}
}
}
//判断是否等于预期结果
$expressionResult = $this->getExpressionResult($expression);
if($this->result == $expressionResult){
echo $expression . " = ". $expressionResult, PHP_EOL;
}
}
}
//根据字符串表达式计算结果
public function getExpressionResult($expression)
{
//将加减符号进行分解排序
$all = str_split($expression,1);
$flag_reduce = array_keys($all,'-');
$flag_add = array_keys($all,'+');
$flags = array_merge($flag_add,$flag_reduce);
asort($flags);
foreach($flags as $key => $value){
array_search($value,$flag_reduce) === false ? $flags[$key] = "+":$flags[$key] = "-";
}
//重建key
$flags = array_values($flags);
//按顺序获得运算数
$expression_reduce = str_replace("+","-",$expression);
$array_numbers = explode('-',$expression_reduce);
//逐个数字进行运算
$result = 0;
foreach($array_numbers as $k => $v){
if($k == 0){
$result = $v;
continue;
}
$flag = isset($flags[$k-1])?$flags[$k-1]:"";
switch($flag){
case "+":
{
$result = $result + $v;
break;
}
case "-":
{
$result = $result - $v;
break;
}
case "":
{
break;
}
}
}
return $result;
}
public function getResult($base)
{
$this->numberItems = $base;
$this->getSituation(0);
$this->calculate();
}
}
//获取输入变量
$base = explode(' ', trim(fgets(STDIN), " \t\n\r\0\x0B[]"));
$fire = new Fire();
$fire->getResult($base); 查看全部
1 2 3 4 5 6 7 8 9 = ？（举报邮箱前缀数字）;（备注110）
为了使等式成立，需要在数字间填入加号或者减号（可以不填，但不能填入其它符号）。之间没有填入符号的数字组合成一个数，例如：12+34+56+7-8+9 就是一种合格的填法。
请大家帮忙计算出多少个可能组合吧，至少3个以上算有效
示例
输入：[1 2 3 4 5 6 7 8 9 ]
输出：12+34+56+7-8+9
…………………………
【PHP实现】
<?php
class Fire {
private $numberItems = array();
//用于存储所有可能的情况
private $situation = array();
//设计的最终结果
private $result = 110;
//用于存储计算结果和设计结果一直的情况
private $rightSituation = array();
//用0,1,2分别代表空格、加号和减号
private $symbol = array(0=>"",1=>"+",2=>"-");
private $temp = array();
//获取所有可能出现的情况
public function getSituation($index)
{
if ($index == 8) {
$this->situation[] = $this->temp;
return;
}
//每个空有三种可能，0,1,2
for ($i = 0; $i < 3; $i++) {
$this->temp[$index] = $i;
$this->getSituation($index + 1);
$this->temp[$index] = 0; //恢复原来的状态
}
}
//获得表达式和输出结果
public function calculate()
{
foreach($this->situation as $k => $v){
$number = 1;
$expression = 1;
foreach($v as $key => $value){
switch($value)
{
//空格
case 0:
{
$expression = $expression.$this->numberItems[$key+1];
break;
}
//加号
case 1:
{
$expression = $expression . "+" .$this->numberItems[$key+1];
break;
}
//减号
case 2:
{
$expression = $expression . "-" .$this->numberItems[$key+1];
break;
}
}
}
//判断是否等于预期结果
$expressionResult = $this->getExpressionResult($expression);
if($this->result == $expressionResult){
echo $expression . " = ". $expressionResult, PHP_EOL;
}
}
}
//根据字符串表达式计算结果
public function getExpressionResult($expression)
{
//将加减符号进行分解排序
$all = str_split($expression,1);
$flag_reduce = array_keys($all,'-');
$flag_add = array_keys($all,'+');
$flags = array_merge($flag_add,$flag_reduce);
asort($flags);
foreach($flags as $key => $value){
array_search($value,$flag_reduce) === false ? $flags[$key] = "+":$flags[$key] = "-";
}
//重建key
$flags = array_values($flags);
//按顺序获得运算数
$expression_reduce = str_replace("+","-",$expression);
$array_numbers = explode('-',$expression_reduce);
//逐个数字进行运算
$result = 0;
foreach($array_numbers as $k => $v){
if($k == 0){
$result = $v;
continue;
}
$flag = isset($flags[$k-1])?$flags[$k-1]:"";
switch($flag){
case "+":
{
$result = $result + $v;
break;
}
case "-":
{
$result = $result - $v;
break;
}
case "":
{
break;
}
}
}
return $result;
}
public function getResult($base)
{
$this->numberItems = $base;
$this->getSituation(0);
$this->calculate();
}
}
//获取输入变量
$base = explode(' ', trim(fgets(STDIN), " \t\n\r\0\x0B[]"));
$fire = new Fire();
$fire->getResult($base); 查看全部
2. 2016年自如将品质管理中心升级为安全与品质管理中心，并开通了自如举报邮箱。请看下边的算式
1 2 3 4 5 6 7 8 9 = ？（举报邮箱前缀数字）;（备注110）
为了使等式成立，需要在数字间填入加号或者减号（可以不填，但不能填入其它符号）。之间没有填入符号的数字组合成一个数，例如：12+34+56+7-8+9 就是一种合格的填法。
请大家帮忙计算出多少个可能组合吧，至少3个以上算有效
示例
输入：[1 2 3 4 5 6 7 8 9 ]
输出：12+34+56+7-8+9
…………………………
【PHP实现】
1 2 3 4 5 6 7 8 9 = ？（举报邮箱前缀数字）;（备注110）
为了使等式成立，需要在数字间填入加号或者减号（可以不填，但不能填入其它符号）。之间没有填入符号的数字组合成一个数，例如：12+34+56+7-8+9 就是一种合格的填法。
请大家帮忙计算出多少个可能组合吧，至少3个以上算有效
示例
输入：[1 2 3 4 5 6 7 8 9 ]
输出：12+34+56+7-8+9
…………………………
【PHP实现】
<?php
class Fire {
private $numberItems = array();
//用于存储所有可能的情况
private $situation = array();
//设计的最终结果
private $result = 110;
//用于存储计算结果和设计结果一直的情况
private $rightSituation = array();
//用0,1,2分别代表空格、加号和减号
private $symbol = array(0=>"",1=>"+",2=>"-");
private $temp = array();
//获取所有可能出现的情况
public function getSituation($index)
{
if ($index == 8) {
$this->situation[] = $this->temp;
return;
}
//每个空有三种可能，0,1,2
for ($i = 0; $i < 3; $i++) {
$this->temp[$index] = $i;
$this->getSituation($index + 1);
$this->temp[$index] = 0; //恢复原来的状态
}
}
//获得表达式和输出结果
public function calculate()
{
foreach($this->situation as $k => $v){
$number = 1;
$expression = 1;
foreach($v as $key => $value){
switch($value)
{
//空格
case 0:
{
$expression = $expression.$this->numberItems[$key+1];
break;
}
//加号
case 1:
{
$expression = $expression . "+" .$this->numberItems[$key+1];
break;
}
//减号
case 2:
{
$expression = $expression . "-" .$this->numberItems[$key+1];
break;
}
}
}
//判断是否等于预期结果
$expressionResult = $this->getExpressionResult($expression);
if($this->result == $expressionResult){
echo $expression . " = ". $expressionResult, PHP_EOL;
}
}
}
//根据字符串表达式计算结果
public function getExpressionResult($expression)
{
//将加减符号进行分解排序
$all = str_split($expression,1);
$flag_reduce = array_keys($all,'-');
$flag_add = array_keys($all,'+');
$flags = array_merge($flag_add,$flag_reduce);
asort($flags);
foreach($flags as $key => $value){
array_search($value,$flag_reduce) === false ? $flags[$key] = "+":$flags[$key] = "-";
}
//重建key
$flags = array_values($flags);
//按顺序获得运算数
$expression_reduce = str_replace("+","-",$expression);
$array_numbers = explode('-',$expression_reduce);
//逐个数字进行运算
$result = 0;
foreach($array_numbers as $k => $v){
if($k == 0){
$result = $v;
continue;
}
$flag = isset($flags[$k-1])?$flags[$k-1]:"";
switch($flag){
case "+":
{
$result = $result + $v;
break;
}
case "-":
{
$result = $result - $v;
break;
}
case "":
{
break;
}
}
}
return $result;
}
public function getResult($base)
{
$this->numberItems = $base;
$this->getSituation(0);
$this->calculate();
}
}
//获取输入变量
$base = explode(' ', trim(fgets(STDIN), " \t\n\r\0\x0B[]"));
$fire = new Fire();
$fire->getResult($base);
2017自如技术大赛研发组题目一：租金卡大放送
PHP • zkbhj 发表了文章 • 0 个评论 • 1521 次浏览 • 2017-12-03 23:58
题目：“司庆大放送，一元即租房”，司庆当日，签约入住的客户，住满30天，返还（首月租金-1元）额度的租金卡。租金卡的面额遵循了类似人民币的固定面额（1000元、500元、100元、50元、20元、10元、5元、1元），请实现一个算法，给客户返还的租金卡张数是最少的。
示例：
输入（租金卡金额）：54 输出：5
【PHP实现】
<?php
/**
* Class Money
* 租金卡张数计算类
* User: 郑凯
* Date: 2017/12/2
* Time: 12:15
*/
class Money {
//租金卡总金额
public $totalValue;
//租金卡面额列表
public $couponList = array(1000=>0,500=>0,100=>0,50=>0,20=>0,10=>0,5=>0,1=>0);
//算法主体，计算当前金额中可以整租的最大基础面额，并计数
private function getMaxValue($money)
{
//按基础面额从高到低依次循环，如果能够被当前金额“整除”，则计算张数并递归
//当金额最后为0时，结束循环，完成计算
foreach ($this->couponList as $key => $value){
if($money / $key >= 1 && $money > 0){
//对应金额数组的个数增加
$this->couponList[$key] = floor($money / $key);
//更新下次计算金额
$money-=$key*floor($money / $key);
//递归调用
$this->getMaxValue($money);
}
}
}
//获取完整列表结果
public function getResult()
{
//调用计算函数进行计算
$this->getMaxValue($this->totalValue);
//输出结果
echo "当总金额为 ".$this->totalValue." 时，需要";
foreach ($this->couponList as $key => $value){
if($value > 0){
echo $value . "张面额为 ".$key." 元的租金卡, ";
}
}
echo "总计 ".array_sum($this->couponList)." 张！";
}
//获取总张数
public function getTotalCounts()
{
return array_sum($this->couponList);
}
}
//获取输入变量
$params = trim(fgets(STDIN), " \t\n\r\0\x0B[]");
//实例化类并初始化类
$myCoupon = new Money();
$myCoupon->totalValue = $params;
$myCoupon->getResult();
//\n是为了让输出结果在anycodes.cn的输出界面可以换行
echo "\n" . $myCoupon->getTotalCounts(); 查看全部
示例：
输入（租金卡金额）：54 输出：5
【PHP实现】
<?php
/**
* Class Money
* 租金卡张数计算类
* User: 郑凯
* Date: 2017/12/2
* Time: 12:15
*/
class Money {
//租金卡总金额
public $totalValue;
//租金卡面额列表
public $couponList = array(1000=>0,500=>0,100=>0,50=>0,20=>0,10=>0,5=>0,1=>0);
//算法主体，计算当前金额中可以整租的最大基础面额，并计数
private function getMaxValue($money)
{
//按基础面额从高到低依次循环，如果能够被当前金额“整除”，则计算张数并递归
//当金额最后为0时，结束循环，完成计算
foreach ($this->couponList as $key => $value){
if($money / $key >= 1 && $money > 0){
//对应金额数组的个数增加
$this->couponList[$key] = floor($money / $key);
//更新下次计算金额
$money-=$key*floor($money / $key);
//递归调用
$this->getMaxValue($money);
}
}
}
//获取完整列表结果
public function getResult()
{
//调用计算函数进行计算
$this->getMaxValue($this->totalValue);
//输出结果
echo "当总金额为 ".$this->totalValue." 时，需要";
foreach ($this->couponList as $key => $value){
if($value > 0){
echo $value . "张面额为 ".$key." 元的租金卡, ";
}
}
echo "总计 ".array_sum($this->couponList)." 张！";
}
//获取总张数
public function getTotalCounts()
{
return array_sum($this->couponList);
}
}
//获取输入变量
$params = trim(fgets(STDIN), " \t\n\r\0\x0B[]");
//实例化类并初始化类
$myCoupon = new Money();
$myCoupon->totalValue = $params;
$myCoupon->getResult();
//\n是为了让输出结果在anycodes.cn的输出界面可以换行
echo "\n" . $myCoupon->getTotalCounts(); 查看全部
题目：“司庆大放送，一元即租房”，司庆当日，签约入住的客户，住满30天，返还（首月租金-1元）额度的租金卡。租金卡的面额遵循了类似人民币的固定面额（1000元、500元、100元、50元、20元、10元、5元、1元），请实现一个算法，给客户返还的租金卡张数是最少的。
示例：
输入（租金卡金额）：54 输出：5
【PHP实现】
示例：
输入（租金卡金额）：54 输出：5
【PHP实现】
<?php
/**
* Class Money
* 租金卡张数计算类
* User: 郑凯
* Date: 2017/12/2
* Time: 12:15
*/
class Money {
//租金卡总金额
public $totalValue;
//租金卡面额列表
public $couponList = array(1000=>0,500=>0,100=>0,50=>0,20=>0,10=>0,5=>0,1=>0);
//算法主体，计算当前金额中可以整租的最大基础面额，并计数
private function getMaxValue($money)
{
//按基础面额从高到低依次循环，如果能够被当前金额“整除”，则计算张数并递归
//当金额最后为0时，结束循环，完成计算
foreach ($this->couponList as $key => $value){
if($money / $key >= 1 && $money > 0){
//对应金额数组的个数增加
$this->couponList[$key] = floor($money / $key);
//更新下次计算金额
$money-=$key*floor($money / $key);
//递归调用
$this->getMaxValue($money);
}
}
}
//获取完整列表结果
public function getResult()
{
//调用计算函数进行计算
$this->getMaxValue($this->totalValue);
//输出结果
echo "当总金额为 ".$this->totalValue." 时，需要";
foreach ($this->couponList as $key => $value){
if($value > 0){
echo $value . "张面额为 ".$key." 元的租金卡, ";
}
}
echo "总计 ".array_sum($this->couponList)." 张！";
}
//获取总张数
public function getTotalCounts()
{
return array_sum($this->couponList);
}
}
//获取输入变量
$params = trim(fgets(STDIN), " \t\n\r\0\x0B[]");
//实例化类并初始化类
$myCoupon = new Money();
$myCoupon->totalValue = $params;
$myCoupon->getResult();
//\n是为了让输出结果在anycodes.cn的输出界面可以换行
echo "\n" . $myCoupon->getTotalCounts();
#2020学习打卡##C程序设计语言# C语言实现快速排序
C语言 • zkbhj 发表了文章 • 0 个评论 • 1265 次浏览 • 2020-04-23 17:24
关于什么是快速排序，可以参考文章 ：什么是快速排序。里面有介绍快速排序的方法以及和冒泡排序的区别，还有PHP版本实现快速排序的方法。本文章只讨论C语言实现的一种方式。#include <stdio.h>
//快速排序算法(从小到大)
//arr:需要排序的数组，begin:需要排序的区间左边界，end:需要排序的区间的右边界
void quickSort(int *arr,int begin,int end)
{
//如果区间不只一个数
if(begin < end)
{
int temp = arr[begin]; //将区间的第一个数作为基准数
int i = begin; //从左到右进行查找时的“指针”，指示当前左位置
int j = end; //从右到左进行查找时的“指针”，指示当前右位置
//不重复遍历
while(i < j)
{
//当右边的数大于基准数时，略过，继续向左查找
//不满足条件时跳出循环，此时的j对应的元素是小于基准元素的
while(i<j && arr[j] > temp)
j--;
//将右边小于等于基准元素的数填入右边相应位置
arr[i] = arr[j];
//当左边的数小于等于基准数时，略过，继续向右查找
//(重复的基准元素集合到左区间)
//不满足条件时跳出循环，此时的i对应的元素是大于等于基准元素的
while(i<j && arr[i] <= temp)
i++;
//将左边大于基准元素的数填入左边相应位置
arr[j] = arr[i];
}
//将基准元素填入相应位置
arr[i] = temp;
//此时的i即为基准元素的位置
//对基准元素的左边子区间进行相似的快速排序
quickSort(arr,begin,i-1);
//对基准元素的右边子区间进行相似的快速排序
quickSort(arr,i+1,end);
}
//如果区间只有一个数，则返回
else
return;
}
int main()
{
int num[12] = {23,45,17,11,13,89,72,26,3,17,11,13};
int n = 12;
quickSort(num,0,n-1);
printf("排序后的数组为：\n");
// for(int i=0;i<n;i++)
// printf("%d ", num[i]);
int *p = num;
while(n>0) {
n--;
printf("%d ",*p++);
}
return 0;
}
[/i][/i][/i][/i][/i][i][i][i][i]https://github.com/happy-hacki ... ort.c[/i][/i][/i][/i] 查看全部
//快速排序算法(从小到大)
//arr:需要排序的数组，begin:需要排序的区间左边界，end:需要排序的区间的右边界
void quickSort(int *arr,int begin,int end)
{
//如果区间不只一个数
if(begin < end)
{
int temp = arr[begin]; //将区间的第一个数作为基准数
int i = begin; //从左到右进行查找时的“指针”，指示当前左位置
int j = end; //从右到左进行查找时的“指针”，指示当前右位置
//不重复遍历
while(i < j)
{
//当右边的数大于基准数时，略过，继续向左查找
//不满足条件时跳出循环，此时的j对应的元素是小于基准元素的
while(i<j && arr[j] > temp)
j--;
//将右边小于等于基准元素的数填入右边相应位置
arr[i] = arr[j];
//当左边的数小于等于基准数时，略过，继续向右查找
//(重复的基准元素集合到左区间)
//不满足条件时跳出循环，此时的i对应的元素是大于等于基准元素的
while(i<j && arr[i] <= temp)
i++;
//将左边大于基准元素的数填入左边相应位置
arr[j] = arr[i];
}
//将基准元素填入相应位置
arr[i] = temp;
//此时的i即为基准元素的位置
//对基准元素的左边子区间进行相似的快速排序
quickSort(arr,begin,i-1);
//对基准元素的右边子区间进行相似的快速排序
quickSort(arr,i+1,end);
}
//如果区间只有一个数，则返回
else
return;
}
int main()
{
int num[12] = {23,45,17,11,13,89,72,26,3,17,11,13};
int n = 12;
quickSort(num,0,n-1);
printf("排序后的数组为：\n");
// for(int i=0;i<n;i++)
// printf("%d ", num[i]);
int *p = num;
while(n>0) {
n--;
printf("%d ",*p++);
}
return 0;
}
[/i][/i][/i][/i][/i][i][i][i][i]https://github.com/happy-hacki ... ort.c[/i][/i][/i][/i] 查看全部
关于什么是快速排序，可以参考文章 ：什么是快速排序。里面有介绍快速排序的方法以及和冒泡排序的区别，还有PHP版本实现快速排序的方法。本文章只讨论C语言实现的一种方式。
#include <stdio.h>[i][i][i][i]https://github.com/happy-hacki ... ort.c[/i][/i][/i][/i]
//快速排序算法(从小到大)
//arr:需要排序的数组，begin:需要排序的区间左边界，end:需要排序的区间的右边界
void quickSort(int *arr,int begin,int end)
{
//如果区间不只一个数
if(begin < end)
{
int temp = arr[begin]; //将区间的第一个数作为基准数
int i = begin; //从左到右进行查找时的“指针”，指示当前左位置
int j = end; //从右到左进行查找时的“指针”，指示当前右位置
//不重复遍历
while(i < j)
{
//当右边的数大于基准数时，略过，继续向左查找
//不满足条件时跳出循环，此时的j对应的元素是小于基准元素的
while(i<j && arr[j] > temp)
j--;
//将右边小于等于基准元素的数填入右边相应位置
arr[i] = arr[j];
//当左边的数小于等于基准数时，略过，继续向右查找
//(重复的基准元素集合到左区间)
//不满足条件时跳出循环，此时的i对应的元素是大于等于基准元素的
while(i<j && arr[i] <= temp)
i++;
//将左边大于基准元素的数填入左边相应位置
arr[j] = arr[i];
}
//将基准元素填入相应位置
arr[i] = temp;
//此时的i即为基准元素的位置
//对基准元素的左边子区间进行相似的快速排序
quickSort(arr,begin,i-1);
//对基准元素的右边子区间进行相似的快速排序
quickSort(arr,i+1,end);
}
//如果区间只有一个数，则返回
else
return;
}
int main()
{
int num[12] = {23,45,17,11,13,89,72,26,3,17,11,13};
int n = 12;
quickSort(num,0,n-1);
printf("排序后的数组为：\n");
// for(int i=0;i<n;i++)
// printf("%d ", num[i]);
int *p = num;
while(n>0) {
n--;
printf("%d ",*p++);
}
return 0;
}
[/i][/i][/i][/i][/i]
#2020学习打卡##C程序设计语言# 直接插入排序和改进版Shell排序解析
C语言 • zkbhj 发表了文章 • 0 个评论 • 1177 次浏览 • 2020-04-14 17:54
一、直接插入排序
直接插入排序（Straight Insertion Sort）是一种最简单的排序方法，其基本操作是将一条记录插入到已排好的有序表中，从而得到一个新的、记录数量增1的有序表。直接插入排序的时间复杂度为 O(n2)。
实例如下所示：
定义的数组 ： {23,34,56,78,65,90,88,92,18,21}
过程如下所示：
【23】 34 56 78 65 90 88 92 18 21
第 1 次排序结果： 【23 34】 56 78 65 90 88 92 18 21
——用34插入到【23】序列中，34>23，故插入后的顺序是【23，34】
第 2 次排序结果： 【 23 34 56 】78 65 90 88 92 18 21
——用56插入到【23，34】序列中，56>34，故插入后的顺序是【23，34，56】
第 3 次排序结果： 【23 34 56 78】65 90 88 92 18 21
——用78插入到【23，34，56】序列中，78>56，故插入后的顺序是【23，34，56，78】
第 4 次排序结果： 【23 34 56 65 78 】90 88 92 18 21
——用65插入到【23，34，56，78】序列中，65<78，所以78后移一位，和56比较，65>56,故插入后的顺序是【23，34，56，65, 78】
第 5 次排序结果： 【23 34 56 65 78 90 】 88 92 18 21
——用90插入到【23，34，56，65, 78】序列中，78<90 ,故插入后的顺序是【23 34 56 65 78 90 】
第 6 次排序结果： 23 34 56 65 78 88 90 92 18 21
——用88插入到【23 34 56 65 78 90 】序列中，90>88 ,所以90后移一位,故插入后的顺序是【23 34 56 65 78 88 90】
第 7 次排序结果： 23 34 56 65 78 88 90 92 18 21
——用92插入到【23 34 56 65 78 90 】序列中，90<92 ,故插入后的顺序是【23 34 56 65 78 90 92 】
第 8 次排序结果： 18 23 34 56 65 78 88 90 92 21
——用18插入到【23 34 56 65 78 90 92 】序列中，18<92，所以92后移一位，和90比较，90>18,依次后移，直到第一位23，因为18<23, 故插入后的顺序是【18 23 34 56 65 78 88 90 92】
第 9 次排序结果： 18 21 23 34 56 65 78 88 90 92
——用21插入到【23 34 56 65 78 90 92 】序列中，21<92，故92后移一位，和90比较，90>21,依次后移，直到第一位18，因为18<21, 故插入后的顺序是【18 21 23 34 56 65 78 88 90 92】
C语言实现：#include <stdio.h>
//自定义的输出函数
void print(int a, int n ,int i){
printf("%d:",i);
for(int j=0; j<8; j++){
printf("%d",a[j]);
}
printf("\n");
}
//直接插入排序函数
void InsertSort(int a, int n)
{
for(int i= 1; i<n; i++){
if(a < a[i-1]){//若第 i 个元素大于 i-1 元素则直接插入；反之，需要找到适当的插入位置后在插入。
int j= i-1;
int x = a;
while(j>-1 && x < a[j]){ //采用顺序查找方式找到插入的位置，在查找的同时，将数组中的元素进行后移操作，给插入元素腾出空间
a[j+1] = a[j];
j--;
}
a[j+1] = x; //插入到正确位置
}
print(a,n,i);//打印每次排序后的结果
}
}
int main(){
int a[8] = {3,1,7,5,2,4,9,6};
InsertSort(a,8);
return 0;
}
二、Shell排序：直接插入排序算法的一种高速而稳定的改进版本
希尔排序，也称递减增量排序算法，是一种插入排序算法，它出自D.L.Shell，因此而得名。Shell排序又称作缩小增量排序。Shell排序的执行时间依赖于增量序列。
希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。
先取一个小于n的整数d1作为第一个增量，把文件的全部记录分组。所有距离为d1的倍数的记录放在同一个组中。先在各组内进行直接插入排序；然后，取第二个增量d2<d1重复上述的分组和排序，直至所取的增量=1(<…<d2<d1)，即所有记录放在同一组中进行直接插入排序为止。
Shell排序算法的特点
希尔排序是基于插入排序的以下两点性质而提出改进方法的：
插入排序在对几乎已经排好序的数据操作时， 效率高， 即可以达到线性排序的效率[list][*]但插入排序一般来说是低效的， 因为插入排序每次只能将数据移动一位
[/*]
[/list]
时间复杂度：最坏情况下为O(n^2)，平均时间复杂度为O(nlogn)；
空间复杂度：归并排序需要一个大小为1的临时存储空间用以保存合并序列，所以空间复杂度为O(1)
算法稳定性：从上面图片中可以看出，数字5在排序后交换了位置，所以它是不稳定的算法。
例如：12、5、9、34、6、8、33、56、89、0、7、4、22、55、77
具体步骤：
void Shell(int *arr,int len,int gap)
{
for(int i = gap;i < len;i++)
{
int temp = arr;
int j = 0;
for(j = i-gap;j >= 0;j-=gap)
{
if(arr[j] > temp)
{
arr[j+gap] = arr[j];
}
else
{
break;
}
}
arr[j+gap] = temp;
}
}
void Shell_Sort(int *arr,int len)
{
int drr = {5,3,1}; //drr为分的组数，这里5，3，1不固定，但必须相互为素数，且最后数为1
int lend = sizeof(drr)/sizeof(drr[0]);
for(int i = 0;i < lend;i++)
{
Shell(arr,len,drr);
}
}
引用文章：
https://blog.csdn.net/FDk_LCL/java/article/details/90581904
https://www.cnblogs.com/guopengxia0719/p/10520561.html
https://www.cnblogs.com/BaoZiY/p/10931406.html
查看全部
直接插入排序（Straight Insertion Sort）是一种最简单的排序方法，其基本操作是将一条记录插入到已排好的有序表中，从而得到一个新的、记录数量增1的有序表。直接插入排序的时间复杂度为 O(n2)。
实例如下所示：
定义的数组 ： {23,34,56,78,65,90,88,92,18,21}
过程如下所示：
【23】 34 56 78 65 90 88 92 18 21
第 1 次排序结果： 【23 34】 56 78 65 90 88 92 18 21
——用34插入到【23】序列中，34>23，故插入后的顺序是【23，34】
第 2 次排序结果： 【 23 34 56 】78 65 90 88 92 18 21
——用56插入到【23，34】序列中，56>34，故插入后的顺序是【23，34，56】
第 3 次排序结果： 【23 34 56 78】65 90 88 92 18 21
——用78插入到【23，34，56】序列中，78>56，故插入后的顺序是【23，34，56，78】
第 4 次排序结果： 【23 34 56 65 78 】90 88 92 18 21
——用65插入到【23，34，56，78】序列中，65<78，所以78后移一位，和56比较，65>56,故插入后的顺序是【23，34，56，65, 78】
第 5 次排序结果： 【23 34 56 65 78 90 】 88 92 18 21
——用90插入到【23，34，56，65, 78】序列中，78<90 ,故插入后的顺序是【23 34 56 65 78 90 】
第 6 次排序结果： 23 34 56 65 78 88 90 92 18 21
——用88插入到【23 34 56 65 78 90 】序列中，90>88 ,所以90后移一位,故插入后的顺序是【23 34 56 65 78 88 90】
第 7 次排序结果： 23 34 56 65 78 88 90 92 18 21
——用92插入到【23 34 56 65 78 90 】序列中，90<92 ,故插入后的顺序是【23 34 56 65 78 90 92 】
第 8 次排序结果： 18 23 34 56 65 78 88 90 92 21
——用18插入到【23 34 56 65 78 90 92 】序列中，18<92，所以92后移一位，和90比较，90>18,依次后移，直到第一位23，因为18<23, 故插入后的顺序是【18 23 34 56 65 78 88 90 92】
第 9 次排序结果： 18 21 23 34 56 65 78 88 90 92
——用21插入到【23 34 56 65 78 90 92 】序列中，21<92，故92后移一位，和90比较，90>21,依次后移，直到第一位18，因为18<21, 故插入后的顺序是【18 21 23 34 56 65 78 88 90 92】
C语言实现：#include <stdio.h>
//自定义的输出函数
void print(int a, int n ,int i){
printf("%d:",i);
for(int j=0; j<8; j++){
printf("%d",a[j]);
}
printf("\n");
}
//直接插入排序函数
void InsertSort(int a, int n)
{
for(int i= 1; i<n; i++){
if(a < a[i-1]){//若第 i 个元素大于 i-1 元素则直接插入；反之，需要找到适当的插入位置后在插入。
int j= i-1;
int x = a;
while(j>-1 && x < a[j]){ //采用顺序查找方式找到插入的位置，在查找的同时，将数组中的元素进行后移操作，给插入元素腾出空间
a[j+1] = a[j];
j--;
}
a[j+1] = x; //插入到正确位置
}
print(a,n,i);//打印每次排序后的结果
}
}
int main(){
int a[8] = {3,1,7,5,2,4,9,6};
InsertSort(a,8);
return 0;
}
二、Shell排序：直接插入排序算法的一种高速而稳定的改进版本
希尔排序，也称递减增量排序算法，是一种插入排序算法，它出自D.L.Shell，因此而得名。Shell排序又称作缩小增量排序。Shell排序的执行时间依赖于增量序列。
希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。
先取一个小于n的整数d1作为第一个增量，把文件的全部记录分组。所有距离为d1的倍数的记录放在同一个组中。先在各组内进行直接插入排序；然后，取第二个增量d2<d1重复上述的分组和排序，直至所取的增量=1(<…<d2<d1)，即所有记录放在同一组中进行直接插入排序为止。
Shell排序算法的特点
希尔排序是基于插入排序的以下两点性质而提出改进方法的：
插入排序在对几乎已经排好序的数据操作时， 效率高， 即可以达到线性排序的效率[list][*]但插入排序一般来说是低效的， 因为插入排序每次只能将数据移动一位
[/*]
[/list]
时间复杂度：最坏情况下为O(n^2)，平均时间复杂度为O(nlogn)；
空间复杂度：归并排序需要一个大小为1的临时存储空间用以保存合并序列，所以空间复杂度为O(1)
算法稳定性：从上面图片中可以看出，数字5在排序后交换了位置，所以它是不稳定的算法。
例如：12、5、9、34、6、8、33、56、89、0、7、4、22、55、77
具体步骤：
void Shell(int *arr,int len,int gap)
{
for(int i = gap;i < len;i++)
{
int temp = arr;
int j = 0;
for(j = i-gap;j >= 0;j-=gap)
{
if(arr[j] > temp)
{
arr[j+gap] = arr[j];
}
else
{
break;
}
}
arr[j+gap] = temp;
}
}
void Shell_Sort(int *arr,int len)
{
int drr = {5,3,1}; //drr为分的组数，这里5，3，1不固定，但必须相互为素数，且最后数为1
int lend = sizeof(drr)/sizeof(drr[0]);
for(int i = 0;i < lend;i++)
{
Shell(arr,len,drr);
}
}
引用文章：
https://blog.csdn.net/FDk_LCL/java/article/details/90581904
https://www.cnblogs.com/guopengxia0719/p/10520561.html
https://www.cnblogs.com/BaoZiY/p/10931406.html
查看全部
一、直接插入排序
实例如下所示：
定义的数组 ： {23,34,56,78,65,90,88,92,18,21}
过程如下所示：
【23】 34 56 78 65 90 88 92 18 21
第 1 次排序结果： 【23 34】 56 78 65 90 88 92 18 21
——用34插入到【23】序列中，34>23，故插入后的顺序是【23，34】
第 2 次排序结果： 【 23 34 56 】78 65 90 88 92 18 21
——用56插入到【23，34】序列中，56>34，故插入后的顺序是【23，34，56】
第 3 次排序结果： 【23 34 56 78】65 90 88 92 18 21
——用78插入到【23，34，56】序列中，78>56，故插入后的顺序是【23，34，56，78】
第 4 次排序结果： 【23 34 56 65 78 】90 88 92 18 21
——用65插入到【23，34，56，78】序列中，65<78，所以78后移一位，和56比较，65>56,故插入后的顺序是【23，34，56，65, 78】
第 5 次排序结果： 【23 34 56 65 78 90 】 88 92 18 21
——用90插入到【23，34，56，65, 78】序列中，78<90 ,故插入后的顺序是【23 34 56 65 78 90 】
第 6 次排序结果： 23 34 56 65 78 88 90 92 18 21
——用88插入到【23 34 56 65 78 90 】序列中，90>88 ,所以90后移一位,故插入后的顺序是【23 34 56 65 78 88 90】
第 7 次排序结果： 23 34 56 65 78 88 90 92 18 21
——用92插入到【23 34 56 65 78 90 】序列中，90<92 ,故插入后的顺序是【23 34 56 65 78 90 92 】
第 8 次排序结果： 18 23 34 56 65 78 88 90 92 21
——用18插入到【23 34 56 65 78 90 92 】序列中，18<92，所以92后移一位，和90比较，90>18,依次后移，直到第一位23，因为18<23, 故插入后的顺序是【18 23 34 56 65 78 88 90 92】
第 9 次排序结果： 18 21 23 34 56 65 78 88 90 92
——用21插入到【23 34 56 65 78 90 92 】序列中，21<92，故92后移一位，和90比较，90>21,依次后移，直到第一位18，因为18<21, 故插入后的顺序是【18 21 23 34 56 65 78 88 90 92】
C语言实现：
二、Shell排序：直接插入排序算法的一种高速而稳定的改进版本
希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。
先取一个小于n的整数d1作为第一个增量，把文件的全部记录分组。所有距离为d1的倍数的记录放在同一个组中。先在各组内进行直接插入排序；然后，取第二个增量d2<d1重复上述的分组和排序，直至所取的增量=1(<…<d2<d1)，即所有记录放在同一组中进行直接插入排序为止。
Shell排序算法的特点
例如：12、5、9、34、6、8、33、56、89、0、7、4、22、55、77
具体步骤：
引用文章：
https://blog.csdn.net/FDk_LCL/java/article/details/90581904
https://www.cnblogs.com/guopengxia0719/p/10520561.html
https://www.cnblogs.com/BaoZiY/p/10931406.html
直接插入排序（Straight Insertion Sort）是一种最简单的排序方法，其基本操作是将一条记录插入到已排好的有序表中，从而得到一个新的、记录数量增1的有序表。直接插入排序的时间复杂度为 O(n2)。
实例如下所示：
定义的数组 ： {23,34,56,78,65,90,88,92,18,21}
过程如下所示：
【23】 34 56 78 65 90 88 92 18 21
第 1 次排序结果： 【23 34】 56 78 65 90 88 92 18 21
——用34插入到【23】序列中，34>23，故插入后的顺序是【23，34】
第 2 次排序结果： 【 23 34 56 】78 65 90 88 92 18 21
——用56插入到【23，34】序列中，56>34，故插入后的顺序是【23，34，56】
第 3 次排序结果： 【23 34 56 78】65 90 88 92 18 21
——用78插入到【23，34，56】序列中，78>56，故插入后的顺序是【23，34，56，78】
第 4 次排序结果： 【23 34 56 65 78 】90 88 92 18 21
——用65插入到【23，34，56，78】序列中，65<78，所以78后移一位，和56比较，65>56,故插入后的顺序是【23，34，56，65, 78】
第 5 次排序结果： 【23 34 56 65 78 90 】 88 92 18 21
——用90插入到【23，34，56，65, 78】序列中，78<90 ,故插入后的顺序是【23 34 56 65 78 90 】
第 6 次排序结果： 23 34 56 65 78 88 90 92 18 21
——用88插入到【23 34 56 65 78 90 】序列中，90>88 ,所以90后移一位,故插入后的顺序是【23 34 56 65 78 88 90】
第 7 次排序结果： 23 34 56 65 78 88 90 92 18 21
——用92插入到【23 34 56 65 78 90 】序列中，90<92 ,故插入后的顺序是【23 34 56 65 78 90 92 】
第 8 次排序结果： 18 23 34 56 65 78 88 90 92 21
——用18插入到【23 34 56 65 78 90 92 】序列中，18<92，所以92后移一位，和90比较，90>18,依次后移，直到第一位23，因为18<23, 故插入后的顺序是【18 23 34 56 65 78 88 90 92】
第 9 次排序结果： 18 21 23 34 56 65 78 88 90 92
——用21插入到【23 34 56 65 78 90 92 】序列中，21<92，故92后移一位，和90比较，90>21,依次后移，直到第一位18，因为18<21, 故插入后的顺序是【18 21 23 34 56 65 78 88 90 92】
C语言实现：
#include <stdio.h>
//自定义的输出函数
void print(int a, int n ,int i){
printf("%d:",i);
for(int j=0; j<8; j++){
printf("%d",a[j]);
}
printf("\n");
}
//直接插入排序函数
void InsertSort(int a, int n)
{
for(int i= 1; i<n; i++){
if(a < a[i-1]){//若第 i 个元素大于 i-1 元素则直接插入；反之，需要找到适当的插入位置后在插入。
int j= i-1;
int x = a;
while(j>-1 && x < a[j]){ //采用顺序查找方式找到插入的位置，在查找的同时，将数组中的元素进行后移操作，给插入元素腾出空间
a[j+1] = a[j];
j--;
}
a[j+1] = x; //插入到正确位置
}
print(a,n,i);//打印每次排序后的结果
}
}
int main(){
int a[8] = {3,1,7,5,2,4,9,6};
InsertSort(a,8);
return 0;
}
二、Shell排序：直接插入排序算法的一种高速而稳定的改进版本
希尔排序，也称递减增量排序算法，是一种插入排序算法，它出自D.L.Shell，因此而得名。Shell排序又称作缩小增量排序。Shell排序的执行时间依赖于增量序列。
希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。
先取一个小于n的整数d1作为第一个增量，把文件的全部记录分组。所有距离为d1的倍数的记录放在同一个组中。先在各组内进行直接插入排序；然后，取第二个增量d2<d1重复上述的分组和排序，直至所取的增量=1(<…<d2<d1)，即所有记录放在同一组中进行直接插入排序为止。
Shell排序算法的特点
希尔排序是基于插入排序的以下两点性质而提出改进方法的：
- 插入排序在对几乎已经排好序的数据操作时， 效率高， 即可以达到线性排序的效率[list][*]但插入排序一般来说是低效的， 因为插入排序每次只能将数据移动一位
[/*]
[/list]
时间复杂度：最坏情况下为O(n^2)，平均时间复杂度为O(nlogn)；
空间复杂度：归并排序需要一个大小为1的临时存储空间用以保存合并序列，所以空间复杂度为O(1)
算法稳定性：从上面图片中可以看出，数字5在排序后交换了位置，所以它是不稳定的算法。
例如：12、5、9、34、6、8、33、56、89、0、7、4、22、55、77
具体步骤：
void Shell(int *arr,int len,int gap)
{
for(int i = gap;i < len;i++)
{
int temp = arr;
int j = 0;
for(j = i-gap;j >= 0;j-=gap)
{
if(arr[j] > temp)
{
arr[j+gap] = arr[j];
}
else
{
break;
}
}
arr[j+gap] = temp;
}
}
void Shell_Sort(int *arr,int len)
{
int drr = {5,3,1}; //drr为分的组数，这里5，3，1不固定，但必须相互为素数，且最后数为1
int lend = sizeof(drr)/sizeof(drr[0]);
for(int i = 0;i < lend;i++)
{
Shell(arr,len,drr);
}
}
引用文章：
https://blog.csdn.net/FDk_LCL/java/article/details/90581904
https://www.cnblogs.com/guopengxia0719/p/10520561.html
https://www.cnblogs.com/BaoZiY/p/10931406.html
2017自如技术大赛研发组题目七：单源最短路径算法问题
PHP • zkbhj 发表了文章 • 0 个评论 • 1881 次浏览 • 2017-12-04 00:08
7. 自如今年年底就会拥有50W间房子，大家知道每间房房子都是需要配置完才能出租给自如客的，整个房租的配置过程是很复杂的，每天都需要大量的物流师傅将家电，家具等物品从仓库送到需要配置的每个房间。为了能在更多的时间配置更多的房子，我要不断的优化物流从仓库A到房间G的路径或者仓库B到房间E的距离，请写出一种算法给你任意图中两点，计算出两点之间的最短距离。
注：A B C D E F G H 都可能是仓库或者房间，点与点之间是距离
示例：
输入：AE
输出：最短距离：22
【PHP实现】<?php
/**
* Class Road
* 两点间最短路径计算类
* User: 郑凯
* Date: 2017/12/2
* Time: 19:48
* Dijkstra 算法，迪科斯彻算法（Dijkstra），又称为单源最短路径算法。
* Dijstra算法是运用贪心的策略，从源点开始，不断地通过相联通的点找出到其他点的最短距离。
*/
class Road {
//节点对应的字母名
public $pointName = array(
0 => "A",
1 => "B",
2 => "C",
3 => "D",
4 => "E",
5 => "F",
6 => "G",
7 => "H",
);
//地图上的点已经点之间的路径长度
public $points = array(
"A" => array(
"A" => 0,
"B" => 15,
"C" => 6,
"D" => 0,
"E" =>0,
"F" =>25,
"G" =>0,
"H" =>0
),
"B" => array(
"A" => 15,
"B" => 0,
"C" => 9,
"D" => 0,
"E" =>7,
"F" =>0,
"G" =>0,
"H" =>0
),
"C" => array(
"A" => 6,
"B" => 9,
"C" => 0,
"D" => 11,
"E" =>0,
"F" =>0,
"G" =>0,
"H" =>0
),
"D" => array(
"A" => 0,
"B" => 0,
"C" => 11,
"D" => 0,
"E" =>12,
"F" =>0,
"G" =>0,
"H" =>5
),
"E" => array(
"A" => 0,
"B" => 7,
"C" => 0,
"D" => 12,
"E" =>0,
"F" =>5,
"G" =>0,
"H" =>7
),
"F" => array(
"A" => 25,
"B" => 0,
"C" => 0,
"D" => 0,
"E" =>5,
"F" =>0,
"G" =>12,
"H" =>0
),
"G" => array(
"A" => 0,
"B" => 0,
"C" => 0,
"D" => 0,
"E" =>0,
"F" =>12,
"G" =>0,
"H" =>17
),
"H" => array(
"A" => 0,
"B" => 0,
"C" => 0,
"D" => 5,
"E" =>7,
"F" =>0,
"G" =>17,
"H" =>0
),
);
//有向图存储
private $graph = array(
array(0,15,6,0,0,25,0,0),
array(15,0,9,0,7,0,0,0),
array(6,9,0,11,0,0,0,0),
array(0,0,11,0,12,0,0,5),
array(0,7,6,12,0,5,0,7),
array(25,0,6,0,5,0,12,0),
array(0,0,0,0,0,12,0,17),
array(0,0,0,5,7,25,17,0)
);
//设置一个无穷大距离的数字
private $soBig = 999999;
private $path = array();
private function getOptimalPath($a, $b)
{
if($a == $b){
return "start and end could not be one point";
}
//读取已经选择的点
$idx = array_keys($this->points);
$a = array_search($a, $idx);
$b = array_search($b, $idx);
//存储路径上节点距离$a点的最小距离
$c = array();
$path = array();
//初始化距离起点最近的节点的最小距离
for($i=1;$i<8;$i++)
{
if($this->graph[$a][$i]>0)
{
$c[$i] = $this->graph[$a][$i];
$path[$i]['name'] = $this->pointName[$a];
$path[$i]['key'] = $a;
}
else
{
$c[$i] = $this->soBig;
}
}
//用于存储已经选择的节点
$selected = array($a);
$all = array(1,2,3,4,5,6,7);
unset($all[$a-1]);
$others = $all;
// n-1次循环完成转移节点任务
for($i=0;$i<count($this->graph)-1;$i++)
{
//查找剩余节点中距离起点最近的节点v
$current_min = $this->soBig;
$current_min_v = 0;
foreach($others as $k=>$v)
{
if($c[$v] < $current_min)
{
$current_min = $c[$v];
$current_min_v = $v;
}
}
//从$others更新顶点到$selected中
array_push($selected,$current_min_v);
array_splice($others,array_search($current_min_v,$others),1);
//更新最短路径
foreach($others as $k=>$u)
{
if($this->graph[$current_min_v][$u]!=0&&$c[$u]>$c[$current_min_v]+$this->graph[$current_min_v][$u])
{
$path[$u]['name'] = $this->pointName[$current_min_v];
$path[$u]['key'] = $current_min_v;
$c[$u] = $c[$current_min_v]+$this->graph[$current_min_v][$u];
}
}
}
$this->getRoadLine($path,$b,$a);
$finalPath = $this->pointName[$a];
foreach(array_reverse($this->path) as $x => $y){
$finalPath.=$y;
}
$finalPath.=$this->pointName[$b];
return $c[$b]." ".$finalPath;
}
//获取路径信息
public function getRoadLine($path,$b,$a)
{
if($path[$b]['key'] !== $a){
$this->path = $path[$b]['name'];
$this->getRoadLine($path,$path[$b]['key'],$a);
}
}
public function getResult($towPoint){
return $this->getOptimalPath(substr($towPoint,0,1),substr($towPoint, -1));
}
}
//获取输入变量
$params = trim(fgets(STDIN), " \t\n\r\0\x0B");
$road = new Road();
echo $road->getResult($params); 查看全部
注：A B C D E F G H 都可能是仓库或者房间，点与点之间是距离
示例：
输入：AE
输出：最短距离：22
【PHP实现】<?php
/**
* Class Road
* 两点间最短路径计算类
* User: 郑凯
* Date: 2017/12/2
* Time: 19:48
* Dijkstra 算法，迪科斯彻算法（Dijkstra），又称为单源最短路径算法。
* Dijstra算法是运用贪心的策略，从源点开始，不断地通过相联通的点找出到其他点的最短距离。
*/
class Road {
//节点对应的字母名
public $pointName = array(
0 => "A",
1 => "B",
2 => "C",
3 => "D",
4 => "E",
5 => "F",
6 => "G",
7 => "H",
);
//地图上的点已经点之间的路径长度
public $points = array(
"A" => array(
"A" => 0,
"B" => 15,
"C" => 6,
"D" => 0,
"E" =>0,
"F" =>25,
"G" =>0,
"H" =>0
),
"B" => array(
"A" => 15,
"B" => 0,
"C" => 9,
"D" => 0,
"E" =>7,
"F" =>0,
"G" =>0,
"H" =>0
),
"C" => array(
"A" => 6,
"B" => 9,
"C" => 0,
"D" => 11,
"E" =>0,
"F" =>0,
"G" =>0,
"H" =>0
),
"D" => array(
"A" => 0,
"B" => 0,
"C" => 11,
"D" => 0,
"E" =>12,
"F" =>0,
"G" =>0,
"H" =>5
),
"E" => array(
"A" => 0,
"B" => 7,
"C" => 0,
"D" => 12,
"E" =>0,
"F" =>5,
"G" =>0,
"H" =>7
),
"F" => array(
"A" => 25,
"B" => 0,
"C" => 0,
"D" => 0,
"E" =>5,
"F" =>0,
"G" =>12,
"H" =>0
),
"G" => array(
"A" => 0,
"B" => 0,
"C" => 0,
"D" => 0,
"E" =>0,
"F" =>12,
"G" =>0,
"H" =>17
),
"H" => array(
"A" => 0,
"B" => 0,
"C" => 0,
"D" => 5,
"E" =>7,
"F" =>0,
"G" =>17,
"H" =>0
),
);
//有向图存储
private $graph = array(
array(0,15,6,0,0,25,0,0),
array(15,0,9,0,7,0,0,0),
array(6,9,0,11,0,0,0,0),
array(0,0,11,0,12,0,0,5),
array(0,7,6,12,0,5,0,7),
array(25,0,6,0,5,0,12,0),
array(0,0,0,0,0,12,0,17),
array(0,0,0,5,7,25,17,0)
);
//设置一个无穷大距离的数字
private $soBig = 999999;
private $path = array();
private function getOptimalPath($a, $b)
{
if($a == $b){
return "start and end could not be one point";
}
//读取已经选择的点
$idx = array_keys($this->points);
$a = array_search($a, $idx);
$b = array_search($b, $idx);
//存储路径上节点距离$a点的最小距离
$c = array();
$path = array();
//初始化距离起点最近的节点的最小距离
for($i=1;$i<8;$i++)
{
if($this->graph[$a][$i]>0)
{
$c[$i] = $this->graph[$a][$i];
$path[$i]['name'] = $this->pointName[$a];
$path[$i]['key'] = $a;
}
else
{
$c[$i] = $this->soBig;
}
}
//用于存储已经选择的节点
$selected = array($a);
$all = array(1,2,3,4,5,6,7);
unset($all[$a-1]);
$others = $all;
// n-1次循环完成转移节点任务
for($i=0;$i<count($this->graph)-1;$i++)
{
//查找剩余节点中距离起点最近的节点v
$current_min = $this->soBig;
$current_min_v = 0;
foreach($others as $k=>$v)
{
if($c[$v] < $current_min)
{
$current_min = $c[$v];
$current_min_v = $v;
}
}
//从$others更新顶点到$selected中
array_push($selected,$current_min_v);
array_splice($others,array_search($current_min_v,$others),1);
//更新最短路径
foreach($others as $k=>$u)
{
if($this->graph[$current_min_v][$u]!=0&&$c[$u]>$c[$current_min_v]+$this->graph[$current_min_v][$u])
{
$path[$u]['name'] = $this->pointName[$current_min_v];
$path[$u]['key'] = $current_min_v;
$c[$u] = $c[$current_min_v]+$this->graph[$current_min_v][$u];
}
}
}
$this->getRoadLine($path,$b,$a);
$finalPath = $this->pointName[$a];
foreach(array_reverse($this->path) as $x => $y){
$finalPath.=$y;
}
$finalPath.=$this->pointName[$b];
return $c[$b]." ".$finalPath;
}
//获取路径信息
public function getRoadLine($path,$b,$a)
{
if($path[$b]['key'] !== $a){
$this->path = $path[$b]['name'];
$this->getRoadLine($path,$path[$b]['key'],$a);
}
}
public function getResult($towPoint){
return $this->getOptimalPath(substr($towPoint,0,1),substr($towPoint, -1));
}
}
//获取输入变量
$params = trim(fgets(STDIN), " \t\n\r\0\x0B");
$road = new Road();
echo $road->getResult($params); 查看全部
7. 自如今年年底就会拥有50W间房子，大家知道每间房房子都是需要配置完才能出租给自如客的，整个房租的配置过程是很复杂的，每天都需要大量的物流师傅将家电，家具等物品从仓库送到需要配置的每个房间。为了能在更多的时间配置更多的房子，我要不断的优化物流从仓库A到房间G的路径或者仓库B到房间E的距离，请写出一种算法给你任意图中两点，计算出两点之间的最短距离。
注：A B C D E F G H 都可能是仓库或者房间，点与点之间是距离
示例：
输入：AE
输出：最短距离：22
【PHP实现】
注：A B C D E F G H 都可能是仓库或者房间，点与点之间是距离
示例：
输入：AE
输出：最短距离：22
【PHP实现】
<?php
/**
* Class Road
* 两点间最短路径计算类
* User: 郑凯
* Date: 2017/12/2
* Time: 19:48
* Dijkstra 算法，迪科斯彻算法（Dijkstra），又称为单源最短路径算法。
* Dijstra算法是运用贪心的策略，从源点开始，不断地通过相联通的点找出到其他点的最短距离。
*/
class Road {
//节点对应的字母名
public $pointName = array(
0 => "A",
1 => "B",
2 => "C",
3 => "D",
4 => "E",
5 => "F",
6 => "G",
7 => "H",
);
//地图上的点已经点之间的路径长度
public $points = array(
"A" => array(
"A" => 0,
"B" => 15,
"C" => 6,
"D" => 0,
"E" =>0,
"F" =>25,
"G" =>0,
"H" =>0
),
"B" => array(
"A" => 15,
"B" => 0,
"C" => 9,
"D" => 0,
"E" =>7,
"F" =>0,
"G" =>0,
"H" =>0
),
"C" => array(
"A" => 6,
"B" => 9,
"C" => 0,
"D" => 11,
"E" =>0,
"F" =>0,
"G" =>0,
"H" =>0
),
"D" => array(
"A" => 0,
"B" => 0,
"C" => 11,
"D" => 0,
"E" =>12,
"F" =>0,
"G" =>0,
"H" =>5
),
"E" => array(
"A" => 0,
"B" => 7,
"C" => 0,
"D" => 12,
"E" =>0,
"F" =>5,
"G" =>0,
"H" =>7
),
"F" => array(
"A" => 25,
"B" => 0,
"C" => 0,
"D" => 0,
"E" =>5,
"F" =>0,
"G" =>12,
"H" =>0
),
"G" => array(
"A" => 0,
"B" => 0,
"C" => 0,
"D" => 0,
"E" =>0,
"F" =>12,
"G" =>0,
"H" =>17
),
"H" => array(
"A" => 0,
"B" => 0,
"C" => 0,
"D" => 5,
"E" =>7,
"F" =>0,
"G" =>17,
"H" =>0
),
);
//有向图存储
private $graph = array(
array(0,15,6,0,0,25,0,0),
array(15,0,9,0,7,0,0,0),
array(6,9,0,11,0,0,0,0),
array(0,0,11,0,12,0,0,5),
array(0,7,6,12,0,5,0,7),
array(25,0,6,0,5,0,12,0),
array(0,0,0,0,0,12,0,17),
array(0,0,0,5,7,25,17,0)
);
//设置一个无穷大距离的数字
private $soBig = 999999;
private $path = array();
private function getOptimalPath($a, $b)
{
if($a == $b){
return "start and end could not be one point";
}
//读取已经选择的点
$idx = array_keys($this->points);
$a = array_search($a, $idx);
$b = array_search($b, $idx);
//存储路径上节点距离$a点的最小距离
$c = array();
$path = array();
//初始化距离起点最近的节点的最小距离
for($i=1;$i<8;$i++)
{
if($this->graph[$a][$i]>0)
{
$c[$i] = $this->graph[$a][$i];
$path[$i]['name'] = $this->pointName[$a];
$path[$i]['key'] = $a;
}
else
{
$c[$i] = $this->soBig;
}
}
//用于存储已经选择的节点
$selected = array($a);
$all = array(1,2,3,4,5,6,7);
unset($all[$a-1]);
$others = $all;
// n-1次循环完成转移节点任务
for($i=0;$i<count($this->graph)-1;$i++)
{
//查找剩余节点中距离起点最近的节点v
$current_min = $this->soBig;
$current_min_v = 0;
foreach($others as $k=>$v)
{
if($c[$v] < $current_min)
{
$current_min = $c[$v];
$current_min_v = $v;
}
}
//从$others更新顶点到$selected中
array_push($selected,$current_min_v);
array_splice($others,array_search($current_min_v,$others),1);
//更新最短路径
foreach($others as $k=>$u)
{
if($this->graph[$current_min_v][$u]!=0&&$c[$u]>$c[$current_min_v]+$this->graph[$current_min_v][$u])
{
$path[$u]['name'] = $this->pointName[$current_min_v];
$path[$u]['key'] = $current_min_v;
$c[$u] = $c[$current_min_v]+$this->graph[$current_min_v][$u];
}
}
}
$this->getRoadLine($path,$b,$a);
$finalPath = $this->pointName[$a];
foreach(array_reverse($this->path) as $x => $y){
$finalPath.=$y;
}
$finalPath.=$this->pointName[$b];
return $c[$b]." ".$finalPath;
}
//获取路径信息
public function getRoadLine($path,$b,$a)
{
if($path[$b]['key'] !== $a){
$this->path = $path[$b]['name'];
$this->getRoadLine($path,$path[$b]['key'],$a);
}
}
public function getResult($towPoint){
return $this->getOptimalPath(substr($towPoint,0,1),substr($towPoint, -1));
}
}
//获取输入变量
$params = trim(fgets(STDIN), " \t\n\r\0\x0B");
$road = new Road();
echo $road->getResult($params);
2017自如技术大赛研发组题目六：木木熊问题（类约瑟夫环问题）
PHP • zkbhj 发表了文章 • 0 个评论 • 1977 次浏览 • 2017-12-04 00:06
6. 每年夏季自如都会组织夏季夏令营活动，每年组委会都会给来京参加夏令营的小朋友准备好多礼物，今年也是如此。
组委会准备了一些小游戏来获得这些礼物，其中有一个游戏是这样的：组委会让小朋友围成一个圈。然后随机制定一个数e,让编号为0的小朋友开始报数。每次喊道e-1的小朋友直接出列，淘汰出局。从本次喊道e-1的下一个小朋友开始，继续从0报数...e-1淘汰出局...一直这样进行....最后进行到最后一个小朋友，这位小朋友可以拿到“熊帅”亲笔签名的“木木”熊毛绒玩具。
(注：小朋友的编号是从0到n-1)
示例：
输入：n=1314 e=520
输出：796
【PHP实现】
<?php
/**
* Created by PhpStorm.
* User: ZKBHJ
* Date: 2017/12/2
* Time: 18:14
*/
class Summer {
//小朋友总数
public $childCounts = 1314;
//小朋友围成的圈儿
public $childCircle = array();
//指定的随机数
public $e = 520;
//初始化围成一个圈儿
private function initCircle()
{
for($i = 0; $i< $this->childCounts; $i++){
$this->childCircle[$i] = $i;
}
}
private function findChild()
{
$index = 0;
for ($i = 2; $i <= $this->childCounts; $i ++) {
$index = ($index + $this->e) % $i;
}
return $index;
}
public function getResult()
{
$this->initCircle();
return $this->findChild();
}
}
//获取输入变量
$params = explode(' ', trim(fgets(STDIN), " \t\n\r\0\x0B[]"));
foreach($params as $k => $v){
$params[$k] = explode('=',$v);
}
$summer = new Summer();
$summer->childCounts = $params[0][1];
$summer->e = $params[1][1];
echo $summer->getResult(); 查看全部
组委会准备了一些小游戏来获得这些礼物，其中有一个游戏是这样的：组委会让小朋友围成一个圈。然后随机制定一个数e,让编号为0的小朋友开始报数。每次喊道e-1的小朋友直接出列，淘汰出局。从本次喊道e-1的下一个小朋友开始，继续从0报数...e-1淘汰出局...一直这样进行....最后进行到最后一个小朋友，这位小朋友可以拿到“熊帅”亲笔签名的“木木”熊毛绒玩具。
(注：小朋友的编号是从0到n-1)
示例：
输入：n=1314 e=520
输出：796
【PHP实现】
<?php
/**
* Created by PhpStorm.
* User: ZKBHJ
* Date: 2017/12/2
* Time: 18:14
*/
class Summer {
//小朋友总数
public $childCounts = 1314;
//小朋友围成的圈儿
public $childCircle = array();
//指定的随机数
public $e = 520;
//初始化围成一个圈儿
private function initCircle()
{
for($i = 0; $i< $this->childCounts; $i++){
$this->childCircle[$i] = $i;
}
}
private function findChild()
{
$index = 0;
for ($i = 2; $i <= $this->childCounts; $i ++) {
$index = ($index + $this->e) % $i;
}
return $index;
}
public function getResult()
{
$this->initCircle();
return $this->findChild();
}
}
//获取输入变量
$params = explode(' ', trim(fgets(STDIN), " \t\n\r\0\x0B[]"));
foreach($params as $k => $v){
$params[$k] = explode('=',$v);
}
$summer = new Summer();
$summer->childCounts = $params[0][1];
$summer->e = $params[1][1];
echo $summer->getResult(); 查看全部
6. 每年夏季自如都会组织夏季夏令营活动，每年组委会都会给来京参加夏令营的小朋友准备好多礼物，今年也是如此。
组委会准备了一些小游戏来获得这些礼物，其中有一个游戏是这样的：组委会让小朋友围成一个圈。然后随机制定一个数e,让编号为0的小朋友开始报数。每次喊道e-1的小朋友直接出列，淘汰出局。从本次喊道e-1的下一个小朋友开始，继续从0报数...e-1淘汰出局...一直这样进行....最后进行到最后一个小朋友，这位小朋友可以拿到“熊帅”亲笔签名的“木木”熊毛绒玩具。
(注：小朋友的编号是从0到n-1)
示例：
输入：n=1314 e=520
输出：796
【PHP实现】
组委会准备了一些小游戏来获得这些礼物，其中有一个游戏是这样的：组委会让小朋友围成一个圈。然后随机制定一个数e,让编号为0的小朋友开始报数。每次喊道e-1的小朋友直接出列，淘汰出局。从本次喊道e-1的下一个小朋友开始，继续从0报数...e-1淘汰出局...一直这样进行....最后进行到最后一个小朋友，这位小朋友可以拿到“熊帅”亲笔签名的“木木”熊毛绒玩具。
(注：小朋友的编号是从0到n-1)
示例：
输入：n=1314 e=520
输出：796
【PHP实现】
<?php
/**
* Created by PhpStorm.
* User: ZKBHJ
* Date: 2017/12/2
* Time: 18:14
*/
class Summer {
//小朋友总数
public $childCounts = 1314;
//小朋友围成的圈儿
public $childCircle = array();
//指定的随机数
public $e = 520;
//初始化围成一个圈儿
private function initCircle()
{
for($i = 0; $i< $this->childCounts; $i++){
$this->childCircle[$i] = $i;
}
}
private function findChild()
{
$index = 0;
for ($i = 2; $i <= $this->childCounts; $i ++) {
$index = ($index + $this->e) % $i;
}
return $index;
}
public function getResult()
{
$this->initCircle();
return $this->findChild();
}
}
//获取输入变量
$params = explode(' ', trim(fgets(STDIN), " \t\n\r\0\x0B[]"));
foreach($params as $k => $v){
$params[$k] = explode('=',$v);
}
$summer = new Summer();
$summer->childCounts = $params[0][1];
$summer->e = $params[1][1];
echo $summer->getResult();
2017自如技术大赛研发组题目五：订单最优分配问题
PHP • zkbhj 发表了文章 • 0 个评论 • 1494 次浏览 • 2017-12-04 00:04
5. 服务目前每月会对搬家师傅进行评级，根据师傅的评级排名结果，我们将优先保证最优师傅的全天订单
假设师傅每天工作8个小时，给定一天n个订单，每个订单其占用时间长为Ti,挣取价值为Vi,1
现请您为师傅安排订单，并保证师傅挣取价值最大
输入格式
输入n组数据，每组以逗号分隔并且每一个订单的编号，时长，挣取价值，数字以空格分隔
输出格式
输出争取价值，订单编号，订单编号按照价值由大到小排序，争取价值相同，则按照每小时平均争取价值由大到小排序
输入样例
[MV10001 2 100,MV10002 3 120,MV10003 1 200,MV10004 3 200,MV10005 4 70,MV10006 3 120,MV10007 2 10,MV10008 2 30,MV10009 6 500,MV10010 3 400]
输出样例
800 MV10010 MV10003 MV10004
【PHP实现】
<?php
/**
* Class ServiceOrder
* 服务师傅订单最优分配计算
* User: 郑凯
* Date: 2017/12/2
* Time: 18:13
*/
class ServiceOrder {
//待分配的订单数组
public $orderList = array();
//服务师傅每天的工作时长
public $workTime = 8;
//最终筛选出来的收益最大订单列表
public $finalOrderList = array();
//按照预设好的格式，将数据进行初始化，装填到数组中
public function initOrder($orderList)
{
//去除前后多余的[]
$orderList = substr($orderList, 1);
$orderList = substr($orderList, 0, -1);
$tempArray = explode(",",$orderList);
foreach($tempArray as $key => $value){
$this->orderList[$key] = explode(" ",$value);
}
}
function arraySequence($array, $field, $sort = 'SORT_DESC')
{
$arrSort = array();
foreach ($array as $uniqid => $row) {
foreach ($row as $key => $value) {
$arrSort[$key][$uniqid] = $value;
}
}
array_multisort($arrSort[$field], constant($sort), $array);
return $array;
}
//给师傅按最大收益安排订单
public function planOrder()
{
//计算每个订单的平均赚取收益
foreach($this->orderList as $key => $value){
$this->orderList[$key][3] = $value[2]/$value[1];
}
//将订单按照平均赚取收益由高到低排序
$this->orderList = $this->arraySequence($this->orderList,'3','SORT_DESC');
//按照每日工作时长限制，取收益率最高的头几个订单
$workTime = 0;
foreach($this->orderList as $k => $v){
if($this->workTime - $workTime >= $v[1]){
$this->finalOrderList[] = $v;
$workTime+=$v[1];
}
}
}
public function printOrder()
{
//输出总收益
$string = array_sum(array_map(create_function('$val', 'return $val["2"];'), $this->finalOrderList))." ";
//输出订单编号（按单笔订单收益由高到低排序，相同的，则按照平均赚取收益由高到低排序）
foreach($this->finalOrderList as $k => $v){
$total[$k] = $v[2];
$average[$k] = $v[3];
}
array_multisort($total, SORT_DESC, $average, SORT_DESC, $this->finalOrderList);
//输出订单号
foreach($this->finalOrderList as $k => $v){
$string .= $v[0]." ";
}
return $string;
}
public function getResult()
{
$this->planOrder();
return $this->printOrder();
}
}
//获取输入变量
$orderList = trim(fgets(STDIN), " \t\n\r\0\x0B");
$service = new ServiceOrder();
$service->initOrder($orderList);
echo $service->getResult(); 查看全部
假设师傅每天工作8个小时，给定一天n个订单，每个订单其占用时间长为Ti,挣取价值为Vi,1
现请您为师傅安排订单，并保证师傅挣取价值最大
输入格式
输入n组数据，每组以逗号分隔并且每一个订单的编号，时长，挣取价值，数字以空格分隔
输出格式
输出争取价值，订单编号，订单编号按照价值由大到小排序，争取价值相同，则按照每小时平均争取价值由大到小排序
输入样例
[MV10001 2 100,MV10002 3 120,MV10003 1 200,MV10004 3 200,MV10005 4 70,MV10006 3 120,MV10007 2 10,MV10008 2 30,MV10009 6 500,MV10010 3 400]
输出样例
800 MV10010 MV10003 MV10004
【PHP实现】
<?php
/**
* Class ServiceOrder
* 服务师傅订单最优分配计算
* User: 郑凯
* Date: 2017/12/2
* Time: 18:13
*/
class ServiceOrder {
//待分配的订单数组
public $orderList = array();
//服务师傅每天的工作时长
public $workTime = 8;
//最终筛选出来的收益最大订单列表
public $finalOrderList = array();
//按照预设好的格式，将数据进行初始化，装填到数组中
public function initOrder($orderList)
{
//去除前后多余的[]
$orderList = substr($orderList, 1);
$orderList = substr($orderList, 0, -1);
$tempArray = explode(",",$orderList);
foreach($tempArray as $key => $value){
$this->orderList[$key] = explode(" ",$value);
}
}
function arraySequence($array, $field, $sort = 'SORT_DESC')
{
$arrSort = array();
foreach ($array as $uniqid => $row) {
foreach ($row as $key => $value) {
$arrSort[$key][$uniqid] = $value;
}
}
array_multisort($arrSort[$field], constant($sort), $array);
return $array;
}
//给师傅按最大收益安排订单
public function planOrder()
{
//计算每个订单的平均赚取收益
foreach($this->orderList as $key => $value){
$this->orderList[$key][3] = $value[2]/$value[1];
}
//将订单按照平均赚取收益由高到低排序
$this->orderList = $this->arraySequence($this->orderList,'3','SORT_DESC');
//按照每日工作时长限制，取收益率最高的头几个订单
$workTime = 0;
foreach($this->orderList as $k => $v){
if($this->workTime - $workTime >= $v[1]){
$this->finalOrderList[] = $v;
$workTime+=$v[1];
}
}
}
public function printOrder()
{
//输出总收益
$string = array_sum(array_map(create_function('$val', 'return $val["2"];'), $this->finalOrderList))." ";
//输出订单编号（按单笔订单收益由高到低排序，相同的，则按照平均赚取收益由高到低排序）
foreach($this->finalOrderList as $k => $v){
$total[$k] = $v[2];
$average[$k] = $v[3];
}
array_multisort($total, SORT_DESC, $average, SORT_DESC, $this->finalOrderList);
//输出订单号
foreach($this->finalOrderList as $k => $v){
$string .= $v[0]." ";
}
return $string;
}
public function getResult()
{
$this->planOrder();
return $this->printOrder();
}
}
//获取输入变量
$orderList = trim(fgets(STDIN), " \t\n\r\0\x0B");
$service = new ServiceOrder();
$service->initOrder($orderList);
echo $service->getResult(); 查看全部
5. 服务目前每月会对搬家师傅进行评级，根据师傅的评级排名结果，我们将优先保证最优师傅的全天订单
假设师傅每天工作8个小时，给定一天n个订单，每个订单其占用时间长为Ti,挣取价值为Vi,1
现请您为师傅安排订单，并保证师傅挣取价值最大
输入格式
输入n组数据，每组以逗号分隔并且每一个订单的编号，时长，挣取价值，数字以空格分隔
输出格式
输出争取价值，订单编号，订单编号按照价值由大到小排序，争取价值相同，则按照每小时平均争取价值由大到小排序
输入样例
[MV10001 2 100,MV10002 3 120,MV10003 1 200,MV10004 3 200,MV10005 4 70,MV10006 3 120,MV10007 2 10,MV10008 2 30,MV10009 6 500,MV10010 3 400]
输出样例
800 MV10010 MV10003 MV10004
【PHP实现】
假设师傅每天工作8个小时，给定一天n个订单，每个订单其占用时间长为Ti,挣取价值为Vi,1
现请您为师傅安排订单，并保证师傅挣取价值最大
输入格式
输入n组数据，每组以逗号分隔并且每一个订单的编号，时长，挣取价值，数字以空格分隔
输出格式
输出争取价值，订单编号，订单编号按照价值由大到小排序，争取价值相同，则按照每小时平均争取价值由大到小排序
输入样例
[MV10001 2 100,MV10002 3 120,MV10003 1 200,MV10004 3 200,MV10005 4 70,MV10006 3 120,MV10007 2 10,MV10008 2 30,MV10009 6 500,MV10010 3 400]
输出样例
800 MV10010 MV10003 MV10004
【PHP实现】
<?php
/**
* Class ServiceOrder
* 服务师傅订单最优分配计算
* User: 郑凯
* Date: 2017/12/2
* Time: 18:13
*/
class ServiceOrder {
//待分配的订单数组
public $orderList = array();
//服务师傅每天的工作时长
public $workTime = 8;
//最终筛选出来的收益最大订单列表
public $finalOrderList = array();
//按照预设好的格式，将数据进行初始化，装填到数组中
public function initOrder($orderList)
{
//去除前后多余的[]
$orderList = substr($orderList, 1);
$orderList = substr($orderList, 0, -1);
$tempArray = explode(",",$orderList);
foreach($tempArray as $key => $value){
$this->orderList[$key] = explode(" ",$value);
}
}
function arraySequence($array, $field, $sort = 'SORT_DESC')
{
$arrSort = array();
foreach ($array as $uniqid => $row) {
foreach ($row as $key => $value) {
$arrSort[$key][$uniqid] = $value;
}
}
array_multisort($arrSort[$field], constant($sort), $array);
return $array;
}
//给师傅按最大收益安排订单
public function planOrder()
{
//计算每个订单的平均赚取收益
foreach($this->orderList as $key => $value){
$this->orderList[$key][3] = $value[2]/$value[1];
}
//将订单按照平均赚取收益由高到低排序
$this->orderList = $this->arraySequence($this->orderList,'3','SORT_DESC');
//按照每日工作时长限制，取收益率最高的头几个订单
$workTime = 0;
foreach($this->orderList as $k => $v){
if($this->workTime - $workTime >= $v[1]){
$this->finalOrderList[] = $v;
$workTime+=$v[1];
}
}
}
public function printOrder()
{
//输出总收益
$string = array_sum(array_map(create_function('$val', 'return $val["2"];'), $this->finalOrderList))." ";
//输出订单编号（按单笔订单收益由高到低排序，相同的，则按照平均赚取收益由高到低排序）
foreach($this->finalOrderList as $k => $v){
$total[$k] = $v[2];
$average[$k] = $v[3];
}
array_multisort($total, SORT_DESC, $average, SORT_DESC, $this->finalOrderList);
//输出订单号
foreach($this->finalOrderList as $k => $v){
$string .= $v[0]." ";
}
return $string;
}
public function getResult()
{
$this->planOrder();
return $this->printOrder();
}
}
//获取输入变量
$orderList = trim(fgets(STDIN), " \t\n\r\0\x0B");
$service = new ServiceOrder();
$service->initOrder($orderList);
echo $service->getResult();
2017自如技术大赛研发组题目四：蓄水池蓄水量计算问题
PHP • zkbhj 发表了文章 • 0 个评论 • 2025 次浏览 • 2017-12-04 00:02
4. 自如寓打算门口用砖头围立一个蓄水池子，从上面看凹凸不平，凹的地方会有积水。那如果用数字代表每个砖头的高度，就形成一个二维数据（如示例），请问这个池子能存储多少单位的水？
例如二维数组为：
9 9 9 9<br>
3 0 0 9<br>
7 8 9 6<br>
时，答案是中间的0,0位置可以存储3（因为其外面最低是3）个单位的水，因此答案为3+3=6
示例：
输入：[1 1 1 1,1 0 0 1,1 1 1 1]
输出：2
【PHP实现】<?php
/**
* Class Pool
* 蓄水池蓄水量计算类
* User: 郑凯
* Date: 2017/12/2
* Time: 15:35
*/
class WaterPool {
//水池数组(二维数组)
public $poolArray = array();
//水池中凹的地方的数量
public $aoCounts = 0;
//水池中木桶效应的最低“短板”数量（决定单个凹的地方的储水量）
public $bottomCounts = 0;
private function getWater()
{
//遍历水池数组(二维数组)
$bottomTemp = array("height"=>9,"counts"=>0);
foreach($this->poolArray as $key => $value){
foreach($value as $k => $v){
//统计水池中凹的地方的数量
if($v == 0){
$this->aoCounts++;
}
//统计水池中木桶效应的最低“短板”数量
if($bottomTemp["height"] > $v && $v != 0){
$bottomTemp["height"] = $v;
$bottomTemp["counts"] = 1;
}elseif($bottomTemp["height"] == $v){
$bottomTemp["counts"]++;
}
}
}
//计算水池中的最多储水量
return $this->aoCounts * $bottomTemp["height"];
}
//得到结果
public function getResult()
{
return $this->getWater();
}
}
//获取输入变量
$params = explode(',', trim(fgets(STDIN), " \t\n\r\0\x0B"));
foreach($params as $k => $v){
$params[$k] = explode(' ',$v);
}
//实例化
$pool = new WaterPool();
$pool->poolArray = $params;
echo $pool->getResult(); 查看全部
例如二维数组为：
9 9 9 9<br>
3 0 0 9<br>
7 8 9 6<br>
时，答案是中间的0,0位置可以存储3（因为其外面最低是3）个单位的水，因此答案为3+3=6
示例：
输入：[1 1 1 1,1 0 0 1,1 1 1 1]
输出：2
【PHP实现】<?php
/**
* Class Pool
* 蓄水池蓄水量计算类
* User: 郑凯
* Date: 2017/12/2
* Time: 15:35
*/
class WaterPool {
//水池数组(二维数组)
public $poolArray = array();
//水池中凹的地方的数量
public $aoCounts = 0;
//水池中木桶效应的最低“短板”数量（决定单个凹的地方的储水量）
public $bottomCounts = 0;
private function getWater()
{
//遍历水池数组(二维数组)
$bottomTemp = array("height"=>9,"counts"=>0);
foreach($this->poolArray as $key => $value){
foreach($value as $k => $v){
//统计水池中凹的地方的数量
if($v == 0){
$this->aoCounts++;
}
//统计水池中木桶效应的最低“短板”数量
if($bottomTemp["height"] > $v && $v != 0){
$bottomTemp["height"] = $v;
$bottomTemp["counts"] = 1;
}elseif($bottomTemp["height"] == $v){
$bottomTemp["counts"]++;
}
}
}
//计算水池中的最多储水量
return $this->aoCounts * $bottomTemp["height"];
}
//得到结果
public function getResult()
{
return $this->getWater();
}
}
//获取输入变量
$params = explode(',', trim(fgets(STDIN), " \t\n\r\0\x0B"));
foreach($params as $k => $v){
$params[$k] = explode(' ',$v);
}
//实例化
$pool = new WaterPool();
$pool->poolArray = $params;
echo $pool->getResult(); 查看全部
4. 自如寓打算门口用砖头围立一个蓄水池子，从上面看凹凸不平，凹的地方会有积水。那如果用数字代表每个砖头的高度，就形成一个二维数据（如示例），请问这个池子能存储多少单位的水？
例如二维数组为：
9 9 9 9<br>
3 0 0 9<br>
7 8 9 6<br>
时，答案是中间的0,0位置可以存储3（因为其外面最低是3）个单位的水，因此答案为3+3=6
示例：
输入：[1 1 1 1,1 0 0 1,1 1 1 1]
输出：2
【PHP实现】
例如二维数组为：
9 9 9 9<br>
3 0 0 9<br>
7 8 9 6<br>
时，答案是中间的0,0位置可以存储3（因为其外面最低是3）个单位的水，因此答案为3+3=6
示例：
输入：[1 1 1 1,1 0 0 1,1 1 1 1]
输出：2
【PHP实现】
<?php
/**
* Class Pool
* 蓄水池蓄水量计算类
* User: 郑凯
* Date: 2017/12/2
* Time: 15:35
*/
class WaterPool {
//水池数组(二维数组)
public $poolArray = array();
//水池中凹的地方的数量
public $aoCounts = 0;
//水池中木桶效应的最低“短板”数量（决定单个凹的地方的储水量）
public $bottomCounts = 0;
private function getWater()
{
//遍历水池数组(二维数组)
$bottomTemp = array("height"=>9,"counts"=>0);
foreach($this->poolArray as $key => $value){
foreach($value as $k => $v){
//统计水池中凹的地方的数量
if($v == 0){
$this->aoCounts++;
}
//统计水池中木桶效应的最低“短板”数量
if($bottomTemp["height"] > $v && $v != 0){
$bottomTemp["height"] = $v;
$bottomTemp["counts"] = 1;
}elseif($bottomTemp["height"] == $v){
$bottomTemp["counts"]++;
}
}
}
//计算水池中的最多储水量
return $this->aoCounts * $bottomTemp["height"];
}
//得到结果
public function getResult()
{
return $this->getWater();
}
}
//获取输入变量
$params = explode(',', trim(fgets(STDIN), " \t\n\r\0\x0B"));
foreach($params as $k => $v){
$params[$k] = explode(' ',$v);
}
//实例化
$pool = new WaterPool();
$pool->poolArray = $params;
echo $pool->getResult();
2017自如技术大赛研发组题目三：给定数字连接最大数
PHP • zkbhj 发表了文章 • 0 个评论 • 1582 次浏览 • 2017-12-04 00:01
3. 给定一个数组，将数组中的数字连接起来，求最大数。
示例：
输入：4,94,9,14,1
输出：9944141
【PHP实现】
<?php
/**
* Class Max
* 计算最大数字
* User: 郑凯
* Date: 2017/12/2
* Time: 14:02
*/
class Max {
//要进行处理的原始数字数组
public $numbers = array();
//经过处理后排序好的数字数组
public $lastNumber = array();
/**
* 获取整数某个位置的数字值
* @param $number
* @param int $position
* @return bool
*/
public function getPositionNumber($number,$position = 0)
{
//将数字当成字符串，将数字分离个位数存到数组中
for($i=0;$i<strlen($number);$i++){
$array[] = substr($number,$i,1);
}
return isset($array[$position])?$array[$position]:false;
}
/**
* 比较两个数，决定谁优先排在前面（即下面注释中的“最大数”）
* @param $a
* @param $b
* @return null
*/
private function compare($a,$b){
//默认最大值是null
$max = null;
//按两个数中数学概念中的最小数的长度进行从高到低每一位数字的对比
for($i = 0; $i<min(array(strlen($a),strlen($b))); $i++){
//如果同一位上的两个数字相等，则继续向下一位比较
if($this->getPositionNumber($a, $i) == $this->getPositionNumber($b, $i)){
continue;
}else{
//如果两个数字不等，则“最大数”是比较大的那个整数，跳出循环，不再继续比较
$this->getPositionNumber($a, $i) > $this->getPositionNumber($b, $i) ? $max = $a:$max = $b;
break;
}
}
//如果走到这里，说明数学概念中最小数的长度的头几位两个整数一样，那么就需要比较较长数字的下一位和较短数字的第一位
//首先判断这两个整数中哪个是短的
//如果两个整数长度一致，说明两个整数一样，则返回谁都可以
//如果较长数字的下一位比较短整数的第一位大，则“最大数”应该是前者，否则，应该是后者
if($max == null){
if(strlen($a)<strlen($b)){
$this->getPositionNumber($b, $i) > $this->getPositionNumber($a,0) ? $max = $b:$max = $a;
}elseif(strlen($a)>strlen($b)){
$this->getPositionNumber($a, $i) > $this->getPositionNumber($b,0) ? $max = $a:$max = $b;
}else{
$max = $a;
}
}
//返回“最大数”
return $max;
}
//主体函数，获取最大数字
public function getMaxNumber()
{
//初始化最大数，赋值为给定数字数组中的第一个
$max = array("key"=> 0, "value"=>$this->numbers[0]);
//对数组中的每个数字进行循环，将其与Max中的数字进行比较
for($j=0 ;$j < count($this->numbers); $j++){
$tempMax = $this->compare($this->numbers[$j],$max['value']);
//如果得到的“最大数”应不是原来的“最大数”，那么进行最大数的更新（更新key和value），这里的key主要用于下面的unset
if($tempMax != $max['value']){
$max['value'] = $tempMax;
$max['key'] = $j;
}
}
//把这一轮比较中的“最大数”放入数组中
$this->lastNumber[] = $max;
//将这个比较出来的“最大数”从原始数组中删除，不再让他捣乱啦
unset($this->numbers[$max['key']]);
//将原始数组重建key
$this->numbers = array_values($this->numbers);
//如果原始数组中还有数组，继续递归调用
if(count($this->numbers) > 0){
$this->getMaxNumber();
}
}
//输出最后连起来最大的数字
public function getResult()
{
$this->getMaxNumber();
foreach($this->lastNumber as $key => $value){
echo $value['value'];
}
}
}
//获取输入变量
$numbers = explode(',', trim(fgets(STDIN), " \t\n\r\0\x0B[]"));
//实例化
$max = new Max();
$max->numbers = $numbers;
$max->getResult(); 查看全部
示例：
输入：4,94,9,14,1
输出：9944141
【PHP实现】
<?php
/**
* Class Max
* 计算最大数字
* User: 郑凯
* Date: 2017/12/2
* Time: 14:02
*/
class Max {
//要进行处理的原始数字数组
public $numbers = array();
//经过处理后排序好的数字数组
public $lastNumber = array();
/**
* 获取整数某个位置的数字值
* @param $number
* @param int $position
* @return bool
*/
public function getPositionNumber($number,$position = 0)
{
//将数字当成字符串，将数字分离个位数存到数组中
for($i=0;$i<strlen($number);$i++){
$array[] = substr($number,$i,1);
}
return isset($array[$position])?$array[$position]:false;
}
/**
* 比较两个数，决定谁优先排在前面（即下面注释中的“最大数”）
* @param $a
* @param $b
* @return null
*/
private function compare($a,$b){
//默认最大值是null
$max = null;
//按两个数中数学概念中的最小数的长度进行从高到低每一位数字的对比
for($i = 0; $i<min(array(strlen($a),strlen($b))); $i++){
//如果同一位上的两个数字相等，则继续向下一位比较
if($this->getPositionNumber($a, $i) == $this->getPositionNumber($b, $i)){
continue;
}else{
//如果两个数字不等，则“最大数”是比较大的那个整数，跳出循环，不再继续比较
$this->getPositionNumber($a, $i) > $this->getPositionNumber($b, $i) ? $max = $a:$max = $b;
break;
}
}
//如果走到这里，说明数学概念中最小数的长度的头几位两个整数一样，那么就需要比较较长数字的下一位和较短数字的第一位
//首先判断这两个整数中哪个是短的
//如果两个整数长度一致，说明两个整数一样，则返回谁都可以
//如果较长数字的下一位比较短整数的第一位大，则“最大数”应该是前者，否则，应该是后者
if($max == null){
if(strlen($a)<strlen($b)){
$this->getPositionNumber($b, $i) > $this->getPositionNumber($a,0) ? $max = $b:$max = $a;
}elseif(strlen($a)>strlen($b)){
$this->getPositionNumber($a, $i) > $this->getPositionNumber($b,0) ? $max = $a:$max = $b;
}else{
$max = $a;
}
}
//返回“最大数”
return $max;
}
//主体函数，获取最大数字
public function getMaxNumber()
{
//初始化最大数，赋值为给定数字数组中的第一个
$max = array("key"=> 0, "value"=>$this->numbers[0]);
//对数组中的每个数字进行循环，将其与Max中的数字进行比较
for($j=0 ;$j < count($this->numbers); $j++){
$tempMax = $this->compare($this->numbers[$j],$max['value']);
//如果得到的“最大数”应不是原来的“最大数”，那么进行最大数的更新（更新key和value），这里的key主要用于下面的unset
if($tempMax != $max['value']){
$max['value'] = $tempMax;
$max['key'] = $j;
}
}
//把这一轮比较中的“最大数”放入数组中
$this->lastNumber[] = $max;
//将这个比较出来的“最大数”从原始数组中删除，不再让他捣乱啦
unset($this->numbers[$max['key']]);
//将原始数组重建key
$this->numbers = array_values($this->numbers);
//如果原始数组中还有数组，继续递归调用
if(count($this->numbers) > 0){
$this->getMaxNumber();
}
}
//输出最后连起来最大的数字
public function getResult()
{
$this->getMaxNumber();
foreach($this->lastNumber as $key => $value){
echo $value['value'];
}
}
}
//获取输入变量
$numbers = explode(',', trim(fgets(STDIN), " \t\n\r\0\x0B[]"));
//实例化
$max = new Max();
$max->numbers = $numbers;
$max->getResult(); 查看全部
3. 给定一个数组，将数组中的数字连接起来，求最大数。
示例：
输入：4,94,9,14,1
输出：9944141
【PHP实现】
示例：
输入：4,94,9,14,1
输出：9944141
【PHP实现】
<?php
/**
* Class Max
* 计算最大数字
* User: 郑凯
* Date: 2017/12/2
* Time: 14:02
*/
class Max {
//要进行处理的原始数字数组
public $numbers = array();
//经过处理后排序好的数字数组
public $lastNumber = array();
/**
* 获取整数某个位置的数字值
* @param $number
* @param int $position
* @return bool
*/
public function getPositionNumber($number,$position = 0)
{
//将数字当成字符串，将数字分离个位数存到数组中
for($i=0;$i<strlen($number);$i++){
$array[] = substr($number,$i,1);
}
return isset($array[$position])?$array[$position]:false;
}
/**
* 比较两个数，决定谁优先排在前面（即下面注释中的“最大数”）
* @param $a
* @param $b
* @return null
*/
private function compare($a,$b){
//默认最大值是null
$max = null;
//按两个数中数学概念中的最小数的长度进行从高到低每一位数字的对比
for($i = 0; $i<min(array(strlen($a),strlen($b))); $i++){
//如果同一位上的两个数字相等，则继续向下一位比较
if($this->getPositionNumber($a, $i) == $this->getPositionNumber($b, $i)){
continue;
}else{
//如果两个数字不等，则“最大数”是比较大的那个整数，跳出循环，不再继续比较
$this->getPositionNumber($a, $i) > $this->getPositionNumber($b, $i) ? $max = $a:$max = $b;
break;
}
}
//如果走到这里，说明数学概念中最小数的长度的头几位两个整数一样，那么就需要比较较长数字的下一位和较短数字的第一位
//首先判断这两个整数中哪个是短的
//如果两个整数长度一致，说明两个整数一样，则返回谁都可以
//如果较长数字的下一位比较短整数的第一位大，则“最大数”应该是前者，否则，应该是后者
if($max == null){
if(strlen($a)<strlen($b)){
$this->getPositionNumber($b, $i) > $this->getPositionNumber($a,0) ? $max = $b:$max = $a;
}elseif(strlen($a)>strlen($b)){
$this->getPositionNumber($a, $i) > $this->getPositionNumber($b,0) ? $max = $a:$max = $b;
}else{
$max = $a;
}
}
//返回“最大数”
return $max;
}
//主体函数，获取最大数字
public function getMaxNumber()
{
//初始化最大数，赋值为给定数字数组中的第一个
$max = array("key"=> 0, "value"=>$this->numbers[0]);
//对数组中的每个数字进行循环，将其与Max中的数字进行比较
for($j=0 ;$j < count($this->numbers); $j++){
$tempMax = $this->compare($this->numbers[$j],$max['value']);
//如果得到的“最大数”应不是原来的“最大数”，那么进行最大数的更新（更新key和value），这里的key主要用于下面的unset
if($tempMax != $max['value']){
$max['value'] = $tempMax;
$max['key'] = $j;
}
}
//把这一轮比较中的“最大数”放入数组中
$this->lastNumber[] = $max;
//将这个比较出来的“最大数”从原始数组中删除，不再让他捣乱啦
unset($this->numbers[$max['key']]);
//将原始数组重建key
$this->numbers = array_values($this->numbers);
//如果原始数组中还有数组，继续递归调用
if(count($this->numbers) > 0){
$this->getMaxNumber();
}
}
//输出最后连起来最大的数字
public function getResult()
{
$this->getMaxNumber();
foreach($this->lastNumber as $key => $value){
echo $value['value'];
}
}
}
//获取输入变量
$numbers = explode(',', trim(fgets(STDIN), " \t\n\r\0\x0B[]"));
//实例化
$max = new Max();
$max->numbers = $numbers;
$max->getResult();
2017自如技术大赛研发组题目二：110的算式计算
PHP • zkbhj 发表了文章 • 0 个评论 • 1426 次浏览 • 2017-12-04 00:00
2. 2016年自如将品质管理中心升级为安全与品质管理中心，并开通了自如举报邮箱。请看下边的算式
1 2 3 4 5 6 7 8 9 = ？（举报邮箱前缀数字）;（备注110）
为了使等式成立，需要在数字间填入加号或者减号（可以不填，但不能填入其它符号）。之间没有填入符号的数字组合成一个数，例如：12+34+56+7-8+9 就是一种合格的填法。
请大家帮忙计算出多少个可能组合吧，至少3个以上算有效
示例
输入：[1 2 3 4 5 6 7 8 9 ]
输出：12+34+56+7-8+9
…………………………
【PHP实现】
<?php
class Fire {
private $numberItems = array();
//用于存储所有可能的情况
private $situation = array();
//设计的最终结果
private $result = 110;
//用于存储计算结果和设计结果一直的情况
private $rightSituation = array();
//用0,1,2分别代表空格、加号和减号
private $symbol = array(0=>"",1=>"+",2=>"-");
private $temp = array();
//获取所有可能出现的情况
public function getSituation($index)
{
if ($index == 8) {
$this->situation[] = $this->temp;
return;
}
//每个空有三种可能，0,1,2
for ($i = 0; $i < 3; $i++) {
$this->temp[$index] = $i;
$this->getSituation($index + 1);
$this->temp[$index] = 0; //恢复原来的状态
}
}
//获得表达式和输出结果
public function calculate()
{
foreach($this->situation as $k => $v){
$number = 1;
$expression = 1;
foreach($v as $key => $value){
switch($value)
{
//空格
case 0:
{
$expression = $expression.$this->numberItems[$key+1];
break;
}
//加号
case 1:
{
$expression = $expression . "+" .$this->numberItems[$key+1];
break;
}
//减号
case 2:
{
$expression = $expression . "-" .$this->numberItems[$key+1];
break;
}
}
}
//判断是否等于预期结果
$expressionResult = $this->getExpressionResult($expression);
if($this->result == $expressionResult){
echo $expression . " = ". $expressionResult, PHP_EOL;
}
}
}
//根据字符串表达式计算结果
public function getExpressionResult($expression)
{
//将加减符号进行分解排序
$all = str_split($expression,1);
$flag_reduce = array_keys($all,'-');
$flag_add = array_keys($all,'+');
$flags = array_merge($flag_add,$flag_reduce);
asort($flags);
foreach($flags as $key => $value){
array_search($value,$flag_reduce) === false ? $flags[$key] = "+":$flags[$key] = "-";
}
//重建key
$flags = array_values($flags);
//按顺序获得运算数
$expression_reduce = str_replace("+","-",$expression);
$array_numbers = explode('-',$expression_reduce);
//逐个数字进行运算
$result = 0;
foreach($array_numbers as $k => $v){
if($k == 0){
$result = $v;
continue;
}
$flag = isset($flags[$k-1])?$flags[$k-1]:"";
switch($flag){
case "+":
{
$result = $result + $v;
break;
}
case "-":
{
$result = $result - $v;
break;
}
case "":
{
break;
}
}
}
return $result;
}
public function getResult($base)
{
$this->numberItems = $base;
$this->getSituation(0);
$this->calculate();
}
}
//获取输入变量
$base = explode(' ', trim(fgets(STDIN), " \t\n\r\0\x0B[]"));
$fire = new Fire();
$fire->getResult($base); 查看全部
1 2 3 4 5 6 7 8 9 = ？（举报邮箱前缀数字）;（备注110）
为了使等式成立，需要在数字间填入加号或者减号（可以不填，但不能填入其它符号）。之间没有填入符号的数字组合成一个数，例如：12+34+56+7-8+9 就是一种合格的填法。
请大家帮忙计算出多少个可能组合吧，至少3个以上算有效
示例
输入：[1 2 3 4 5 6 7 8 9 ]
输出：12+34+56+7-8+9
…………………………
【PHP实现】
<?php
class Fire {
private $numberItems = array();
//用于存储所有可能的情况
private $situation = array();
//设计的最终结果
private $result = 110;
//用于存储计算结果和设计结果一直的情况
private $rightSituation = array();
//用0,1,2分别代表空格、加号和减号
private $symbol = array(0=>"",1=>"+",2=>"-");
private $temp = array();
//获取所有可能出现的情况
public function getSituation($index)
{
if ($index == 8) {
$this->situation[] = $this->temp;
return;
}
//每个空有三种可能，0,1,2
for ($i = 0; $i < 3; $i++) {
$this->temp[$index] = $i;
$this->getSituation($index + 1);
$this->temp[$index] = 0; //恢复原来的状态
}
}
//获得表达式和输出结果
public function calculate()
{
foreach($this->situation as $k => $v){
$number = 1;
$expression = 1;
foreach($v as $key => $value){
switch($value)
{
//空格
case 0:
{
$expression = $expression.$this->numberItems[$key+1];
break;
}
//加号
case 1:
{
$expression = $expression . "+" .$this->numberItems[$key+1];
break;
}
//减号
case 2:
{
$expression = $expression . "-" .$this->numberItems[$key+1];
break;
}
}
}
//判断是否等于预期结果
$expressionResult = $this->getExpressionResult($expression);
if($this->result == $expressionResult){
echo $expression . " = ". $expressionResult, PHP_EOL;
}
}
}
//根据字符串表达式计算结果
public function getExpressionResult($expression)
{
//将加减符号进行分解排序
$all = str_split($expression,1);
$flag_reduce = array_keys($all,'-');
$flag_add = array_keys($all,'+');
$flags = array_merge($flag_add,$flag_reduce);
asort($flags);
foreach($flags as $key => $value){
array_search($value,$flag_reduce) === false ? $flags[$key] = "+":$flags[$key] = "-";
}
//重建key
$flags = array_values($flags);
//按顺序获得运算数
$expression_reduce = str_replace("+","-",$expression);
$array_numbers = explode('-',$expression_reduce);
//逐个数字进行运算
$result = 0;
foreach($array_numbers as $k => $v){
if($k == 0){
$result = $v;
continue;
}
$flag = isset($flags[$k-1])?$flags[$k-1]:"";
switch($flag){
case "+":
{
$result = $result + $v;
break;
}
case "-":
{
$result = $result - $v;
break;
}
case "":
{
break;
}
}
}
return $result;
}
public function getResult($base)
{
$this->numberItems = $base;
$this->getSituation(0);
$this->calculate();
}
}
//获取输入变量
$base = explode(' ', trim(fgets(STDIN), " \t\n\r\0\x0B[]"));
$fire = new Fire();
$fire->getResult($base); 查看全部
2. 2016年自如将品质管理中心升级为安全与品质管理中心，并开通了自如举报邮箱。请看下边的算式
1 2 3 4 5 6 7 8 9 = ？（举报邮箱前缀数字）;（备注110）
为了使等式成立，需要在数字间填入加号或者减号（可以不填，但不能填入其它符号）。之间没有填入符号的数字组合成一个数，例如：12+34+56+7-8+9 就是一种合格的填法。
请大家帮忙计算出多少个可能组合吧，至少3个以上算有效
示例
输入：[1 2 3 4 5 6 7 8 9 ]
输出：12+34+56+7-8+9
…………………………
【PHP实现】
1 2 3 4 5 6 7 8 9 = ？（举报邮箱前缀数字）;（备注110）
为了使等式成立，需要在数字间填入加号或者减号（可以不填，但不能填入其它符号）。之间没有填入符号的数字组合成一个数，例如：12+34+56+7-8+9 就是一种合格的填法。
请大家帮忙计算出多少个可能组合吧，至少3个以上算有效
示例
输入：[1 2 3 4 5 6 7 8 9 ]
输出：12+34+56+7-8+9
…………………………
【PHP实现】
<?php
class Fire {
private $numberItems = array();
//用于存储所有可能的情况
private $situation = array();
//设计的最终结果
private $result = 110;
//用于存储计算结果和设计结果一直的情况
private $rightSituation = array();
//用0,1,2分别代表空格、加号和减号
private $symbol = array(0=>"",1=>"+",2=>"-");
private $temp = array();
//获取所有可能出现的情况
public function getSituation($index)
{
if ($index == 8) {
$this->situation[] = $this->temp;
return;
}
//每个空有三种可能，0,1,2
for ($i = 0; $i < 3; $i++) {
$this->temp[$index] = $i;
$this->getSituation($index + 1);
$this->temp[$index] = 0; //恢复原来的状态
}
}
//获得表达式和输出结果
public function calculate()
{
foreach($this->situation as $k => $v){
$number = 1;
$expression = 1;
foreach($v as $key => $value){
switch($value)
{
//空格
case 0:
{
$expression = $expression.$this->numberItems[$key+1];
break;
}
//加号
case 1:
{
$expression = $expression . "+" .$this->numberItems[$key+1];
break;
}
//减号
case 2:
{
$expression = $expression . "-" .$this->numberItems[$key+1];
break;
}
}
}
//判断是否等于预期结果
$expressionResult = $this->getExpressionResult($expression);
if($this->result == $expressionResult){
echo $expression . " = ". $expressionResult, PHP_EOL;
}
}
}
//根据字符串表达式计算结果
public function getExpressionResult($expression)
{
//将加减符号进行分解排序
$all = str_split($expression,1);
$flag_reduce = array_keys($all,'-');
$flag_add = array_keys($all,'+');
$flags = array_merge($flag_add,$flag_reduce);
asort($flags);
foreach($flags as $key => $value){
array_search($value,$flag_reduce) === false ? $flags[$key] = "+":$flags[$key] = "-";
}
//重建key
$flags = array_values($flags);
//按顺序获得运算数
$expression_reduce = str_replace("+","-",$expression);
$array_numbers = explode('-',$expression_reduce);
//逐个数字进行运算
$result = 0;
foreach($array_numbers as $k => $v){
if($k == 0){
$result = $v;
continue;
}
$flag = isset($flags[$k-1])?$flags[$k-1]:"";
switch($flag){
case "+":
{
$result = $result + $v;
break;
}
case "-":
{
$result = $result - $v;
break;
}
case "":
{
break;
}
}
}
return $result;
}
public function getResult($base)
{
$this->numberItems = $base;
$this->getSituation(0);
$this->calculate();
}
}
//获取输入变量
$base = explode(' ', trim(fgets(STDIN), " \t\n\r\0\x0B[]"));
$fire = new Fire();
$fire->getResult($base);
2017自如技术大赛研发组题目一：租金卡大放送
PHP • zkbhj 发表了文章 • 0 个评论 • 1521 次浏览 • 2017-12-03 23:58
题目：“司庆大放送，一元即租房”，司庆当日，签约入住的客户，住满30天，返还（首月租金-1元）额度的租金卡。租金卡的面额遵循了类似人民币的固定面额（1000元、500元、100元、50元、20元、10元、5元、1元），请实现一个算法，给客户返还的租金卡张数是最少的。
示例：
输入（租金卡金额）：54 输出：5
【PHP实现】
<?php
/**
* Class Money
* 租金卡张数计算类
* User: 郑凯
* Date: 2017/12/2
* Time: 12:15
*/
class Money {
//租金卡总金额
public $totalValue;
//租金卡面额列表
public $couponList = array(1000=>0,500=>0,100=>0,50=>0,20=>0,10=>0,5=>0,1=>0);
//算法主体，计算当前金额中可以整租的最大基础面额，并计数
private function getMaxValue($money)
{
//按基础面额从高到低依次循环，如果能够被当前金额“整除”，则计算张数并递归
//当金额最后为0时，结束循环，完成计算
foreach ($this->couponList as $key => $value){
if($money / $key >= 1 && $money > 0){
//对应金额数组的个数增加
$this->couponList[$key] = floor($money / $key);
//更新下次计算金额
$money-=$key*floor($money / $key);
//递归调用
$this->getMaxValue($money);
}
}
}
//获取完整列表结果
public function getResult()
{
//调用计算函数进行计算
$this->getMaxValue($this->totalValue);
//输出结果
echo "当总金额为 ".$this->totalValue." 时，需要";
foreach ($this->couponList as $key => $value){
if($value > 0){
echo $value . "张面额为 ".$key." 元的租金卡, ";
}
}
echo "总计 ".array_sum($this->couponList)." 张！";
}
//获取总张数
public function getTotalCounts()
{
return array_sum($this->couponList);
}
}
//获取输入变量
$params = trim(fgets(STDIN), " \t\n\r\0\x0B[]");
//实例化类并初始化类
$myCoupon = new Money();
$myCoupon->totalValue = $params;
$myCoupon->getResult();
//\n是为了让输出结果在anycodes.cn的输出界面可以换行
echo "\n" . $myCoupon->getTotalCounts(); 查看全部
示例：
输入（租金卡金额）：54 输出：5
【PHP实现】
<?php
/**
* Class Money
* 租金卡张数计算类
* User: 郑凯
* Date: 2017/12/2
* Time: 12:15
*/
class Money {
//租金卡总金额
public $totalValue;
//租金卡面额列表
public $couponList = array(1000=>0,500=>0,100=>0,50=>0,20=>0,10=>0,5=>0,1=>0);
//算法主体，计算当前金额中可以整租的最大基础面额，并计数
private function getMaxValue($money)
{
//按基础面额从高到低依次循环，如果能够被当前金额“整除”，则计算张数并递归
//当金额最后为0时，结束循环，完成计算
foreach ($this->couponList as $key => $value){
if($money / $key >= 1 && $money > 0){
//对应金额数组的个数增加
$this->couponList[$key] = floor($money / $key);
//更新下次计算金额
$money-=$key*floor($money / $key);
//递归调用
$this->getMaxValue($money);
}
}
}
//获取完整列表结果
public function getResult()
{
//调用计算函数进行计算
$this->getMaxValue($this->totalValue);
//输出结果
echo "当总金额为 ".$this->totalValue." 时，需要";
foreach ($this->couponList as $key => $value){
if($value > 0){
echo $value . "张面额为 ".$key." 元的租金卡, ";
}
}
echo "总计 ".array_sum($this->couponList)." 张！";
}
//获取总张数
public function getTotalCounts()
{
return array_sum($this->couponList);
}
}
//获取输入变量
$params = trim(fgets(STDIN), " \t\n\r\0\x0B[]");
//实例化类并初始化类
$myCoupon = new Money();
$myCoupon->totalValue = $params;
$myCoupon->getResult();
//\n是为了让输出结果在anycodes.cn的输出界面可以换行
echo "\n" . $myCoupon->getTotalCounts(); 查看全部
题目：“司庆大放送，一元即租房”，司庆当日，签约入住的客户，住满30天，返还（首月租金-1元）额度的租金卡。租金卡的面额遵循了类似人民币的固定面额（1000元、500元、100元、50元、20元、10元、5元、1元），请实现一个算法，给客户返还的租金卡张数是最少的。
示例：
输入（租金卡金额）：54 输出：5
【PHP实现】
示例：
输入（租金卡金额）：54 输出：5
【PHP实现】
<?php
/**
* Class Money
* 租金卡张数计算类
* User: 郑凯
* Date: 2017/12/2
* Time: 12:15
*/
class Money {
//租金卡总金额
public $totalValue;
//租金卡面额列表
public $couponList = array(1000=>0,500=>0,100=>0,50=>0,20=>0,10=>0,5=>0,1=>0);
//算法主体，计算当前金额中可以整租的最大基础面额，并计数
private function getMaxValue($money)
{
//按基础面额从高到低依次循环，如果能够被当前金额“整除”，则计算张数并递归
//当金额最后为0时，结束循环，完成计算
foreach ($this->couponList as $key => $value){
if($money / $key >= 1 && $money > 0){
//对应金额数组的个数增加
$this->couponList[$key] = floor($money / $key);
//更新下次计算金额
$money-=$key*floor($money / $key);
//递归调用
$this->getMaxValue($money);
}
}
}
//获取完整列表结果
public function getResult()
{
//调用计算函数进行计算
$this->getMaxValue($this->totalValue);
//输出结果
echo "当总金额为 ".$this->totalValue." 时，需要";
foreach ($this->couponList as $key => $value){
if($value > 0){
echo $value . "张面额为 ".$key." 元的租金卡, ";
}
}
echo "总计 ".array_sum($this->couponList)." 张！";
}
//获取总张数
public function getTotalCounts()
{
return array_sum($this->couponList);
}
}
//获取输入变量
$params = trim(fgets(STDIN), " \t\n\r\0\x0B[]");
//实例化类并初始化类
$myCoupon = new Money();
$myCoupon->totalValue = $params;
$myCoupon->getResult();
//\n是为了让输出结果在anycodes.cn的输出界面可以换行
echo "\n" . $myCoupon->getTotalCounts();
啊哈！算法！