通知设置 新通知
#2020学习打卡##C程序设计语言# C语言中的随机数函数解析
zkbhj 发表了文章 • 0 个评论 • 1288 次浏览 • 2020-05-25 12:02
在计算机中并没有一个真正的随机数发生器，但是可以做到使产生的数字重复率很低，这样看起来好象是真正的随机数，实现这一功能的程序叫伪随机数发生器。
有关如何产生随机数的理论有许多，如果要详细地讨论，需要厚厚的一本书的篇幅。不管用什么方法实现随机数发生器，都必须给它提供一个名为“种子”的初始值。而且这个值最好是随机的，或者至少这个值是伪随机的。“种子”的值通常是用快速计数寄存器或移位寄存器来生成的。
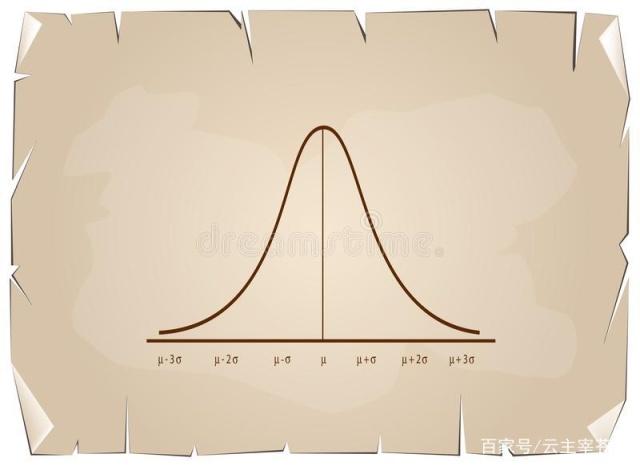
在实际编程中，我们经常会用到随机数这个概念，其实也是一个伪随机数，实际上并不是一个真正的随机数，但是也足够我们使用了。在C语言中，编写一些关于游戏之类的程序时就需要用到随机数了。同时C语言也提供了一个标准库里面一个函数来产生随机数，而对于随机数的产生是根据种子（根据一个数值按照某种公式计算的）来变化的，种子 与随机数之间符合正态分布（高斯分布）。
生成随机数
在C语言中，我们一般使用 <stdlib.h> 头文件中的 rand() 函数来生成随机数，它的用法为：int rand (void);【void是指不需要传递参数】
rand() 会随机生成一个位于 0 ~ RAND_MAX 之间的整数。而对RAND_MAX 是 <stdlib.h> 头文件中的一个宏，它用来指明 rand() 所能返回的随机数的最大值。C语言标准并没有规定 RAND_MAX 的具体数值，只是规定它的值至少为 32767。/**
* 第35堂课示例：随机数
* 郑凯
* 2020年5月25日
* */
#include <stdio.h>
#include <stdlib.h>
int main()
{
int rands;
rands = rand();
printf("rand number is %d\n", rands);
printf("rand number2 is %d\n", rand());
return 0;
}但是这个随机数一旦编译之后就固定了，并不能满足我们的实际需求，前面提到了只是一个伪随机数，我们需要对产生随机数的种子进行不断的重播，从而达到我们实际需求的随机数效果。我们可以通过 srand() 函数来重新“播种”，这样种子就会发生改变。
srand() 的用法为：void srand (unsigned int seed);
它需要一个 unsigned int 类型的参数。在实际开发中，我们可以用时间作为参数，只要每次播种的时间不同，那么生成的种子就不同，最终的随机数也就不同，通常我们采用 <time.h> 头文件中的 time() 函数即可得到当前的时间【精准到秒】srand((unsigned)time(NULL));/**
* 第35堂课示例：随机数
* 郑凯
* 2020年5月25日
* */
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
int main()
{
int rands;
srand((unsigned)time(NULL));
rands = rand();
printf("rand number is %d\n", rands);
printf("rand number2 is %d\n", rand());
return 0;
}小提示：根据种子与随机数的符合高斯分布的关系可知，生成的随机数是逐渐增大或者逐渐减小！
生成一定范围随机数
在实际编程开发中，实际需求往往是一定范围内的随机数，对于产生一定范围的随机数，就需要使用一定的技巧了，常用的方法是取模运算，再加上一个加法运算：int a = rand() % 10; //产生0~9的随机数，注意10会被整除
如果要规定上下限：int a = rand() % 51 + 100; //产生100~150的随机数
分析：取模即取余，rand()%51+13，看成两部分：rand()%51是产生 0~50 的随机数，后面+100保证 a 最小只能是 100，最大就是 50+100=150。/**
* 第35堂课示例：有区间的随机数
* 例如：100~150之间的数字
* 郑凯
* 2020年5月25日
* */
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
int main()
{
int rands;
srand((unsigned)time(NULL));
rands = rand() % 51 + 100;
printf("rand number is %d\n", rands);
return 0;
}
根据种子与随机数的符合高斯分布的关系可知，生成的随机数是逐渐增大或者逐渐减小。 查看全部
有关如何产生随机数的理论有许多，如果要详细地讨论，需要厚厚的一本书的篇幅。不管用什么方法实现随机数发生器，都必须给它提供一个名为“种子”的初始值。而且这个值最好是随机的，或者至少这个值是伪随机的。“种子”的值通常是用快速计数寄存器或移位寄存器来生成的。
在实际编程中，我们经常会用到随机数这个概念，其实也是一个伪随机数，实际上并不是一个真正的随机数，但是也足够我们使用了。在C语言中，编写一些关于游戏之类的程序时就需要用到随机数了。同时C语言也提供了一个标准库里面一个函数来产生随机数，而对于随机数的产生是根据种子（根据一个数值按照某种公式计算的）来变化的，种子 与随机数之间符合正态分布（高斯分布）。
生成随机数
在C语言中，我们一般使用 <stdlib.h> 头文件中的 rand() 函数来生成随机数，它的用法为：int rand (void);【void是指不需要传递参数】
rand() 会随机生成一个位于 0 ~ RAND_MAX 之间的整数。而对RAND_MAX 是 <stdlib.h> 头文件中的一个宏，它用来指明 rand() 所能返回的随机数的最大值。C语言标准并没有规定 RAND_MAX 的具体数值，只是规定它的值至少为 32767。/**
* 第35堂课示例：随机数
* 郑凯
* 2020年5月25日
* */
#include <stdio.h>
#include <stdlib.h>
int main()
{
int rands;
rands = rand();
printf("rand number is %d\n", rands);
printf("rand number2 is %d\n", rand());
return 0;
}但是这个随机数一旦编译之后就固定了，并不能满足我们的实际需求，前面提到了只是一个伪随机数，我们需要对产生随机数的种子进行不断的重播，从而达到我们实际需求的随机数效果。我们可以通过 srand() 函数来重新“播种”，这样种子就会发生改变。
srand() 的用法为：void srand (unsigned int seed);
它需要一个 unsigned int 类型的参数。在实际开发中，我们可以用时间作为参数，只要每次播种的时间不同，那么生成的种子就不同，最终的随机数也就不同，通常我们采用 <time.h> 头文件中的 time() 函数即可得到当前的时间【精准到秒】srand((unsigned)time(NULL));/**
* 第35堂课示例：随机数
* 郑凯
* 2020年5月25日
* */
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
int main()
{
int rands;
srand((unsigned)time(NULL));
rands = rand();
printf("rand number is %d\n", rands);
printf("rand number2 is %d\n", rand());
return 0;
}小提示：根据种子与随机数的符合高斯分布的关系可知，生成的随机数是逐渐增大或者逐渐减小！
生成一定范围随机数
在实际编程开发中，实际需求往往是一定范围内的随机数，对于产生一定范围的随机数，就需要使用一定的技巧了，常用的方法是取模运算，再加上一个加法运算：int a = rand() % 10; //产生0~9的随机数，注意10会被整除
如果要规定上下限：int a = rand() % 51 + 100; //产生100~150的随机数
分析：取模即取余，rand()%51+13，看成两部分：rand()%51是产生 0~50 的随机数，后面+100保证 a 最小只能是 100，最大就是 50+100=150。/**
* 第35堂课示例：有区间的随机数
* 例如：100~150之间的数字
* 郑凯
* 2020年5月25日
* */
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
int main()
{
int rands;
srand((unsigned)time(NULL));
rands = rand() % 51 + 100;
printf("rand number is %d\n", rands);
return 0;
}
根据种子与随机数的符合高斯分布的关系可知，生成的随机数是逐渐增大或者逐渐减小。 查看全部
在计算机中并没有一个真正的随机数发生器，但是可以做到使产生的数字重复率很低，这样看起来好象是真正的随机数，实现这一功能的程序叫伪随机数发生器。
有关如何产生随机数的理论有许多，如果要详细地讨论，需要厚厚的一本书的篇幅。不管用什么方法实现随机数发生器，都必须给它提供一个名为“种子”的初始值。而且这个值最好是随机的，或者至少这个值是伪随机的。“种子”的值通常是用快速计数寄存器或移位寄存器来生成的。
在实际编程中，我们经常会用到随机数这个概念，其实也是一个伪随机数，实际上并不是一个真正的随机数，但是也足够我们使用了。在C语言中，编写一些关于游戏之类的程序时就需要用到随机数了。同时C语言也提供了一个标准库里面一个函数来产生随机数，而对于随机数的产生是根据种子（根据一个数值按照某种公式计算的）来变化的，种子 与随机数之间符合正态分布（高斯分布）。
生成随机数
在C语言中，我们一般使用 <stdlib.h> 头文件中的 rand() 函数来生成随机数，它的用法为：
rand() 会随机生成一个位于 0 ~ RAND_MAX 之间的整数。而对RAND_MAX 是 <stdlib.h> 头文件中的一个宏，它用来指明 rand() 所能返回的随机数的最大值。C语言标准并没有规定 RAND_MAX 的具体数值，只是规定它的值至少为 32767。
srand() 的用法为：
它需要一个 unsigned int 类型的参数。在实际开发中，我们可以用时间作为参数，只要每次播种的时间不同，那么生成的种子就不同，最终的随机数也就不同，通常我们采用 <time.h> 头文件中的 time() 函数即可得到当前的时间【精准到秒】srand((unsigned)time(NULL));
生成一定范围随机数
在实际编程开发中，实际需求往往是一定范围内的随机数，对于产生一定范围的随机数，就需要使用一定的技巧了，常用的方法是取模运算，再加上一个加法运算：
如果要规定上下限：
分析：取模即取余，rand()%51+13，看成两部分：rand()%51是产生 0~50 的随机数，后面+100保证 a 最小只能是 100，最大就是 50+100=150。
根据种子与随机数的符合高斯分布的关系可知，生成的随机数是逐渐增大或者逐渐减小。
有关如何产生随机数的理论有许多，如果要详细地讨论，需要厚厚的一本书的篇幅。不管用什么方法实现随机数发生器，都必须给它提供一个名为“种子”的初始值。而且这个值最好是随机的，或者至少这个值是伪随机的。“种子”的值通常是用快速计数寄存器或移位寄存器来生成的。
在实际编程中，我们经常会用到随机数这个概念，其实也是一个伪随机数，实际上并不是一个真正的随机数，但是也足够我们使用了。在C语言中，编写一些关于游戏之类的程序时就需要用到随机数了。同时C语言也提供了一个标准库里面一个函数来产生随机数，而对于随机数的产生是根据种子（根据一个数值按照某种公式计算的）来变化的，种子 与随机数之间符合正态分布（高斯分布）。
生成随机数
在C语言中，我们一般使用 <stdlib.h> 头文件中的 rand() 函数来生成随机数，它的用法为：
int rand (void);【void是指不需要传递参数】
rand() 会随机生成一个位于 0 ~ RAND_MAX 之间的整数。而对RAND_MAX 是 <stdlib.h> 头文件中的一个宏，它用来指明 rand() 所能返回的随机数的最大值。C语言标准并没有规定 RAND_MAX 的具体数值，只是规定它的值至少为 32767。
/**但是这个随机数一旦编译之后就固定了，并不能满足我们的实际需求，前面提到了只是一个伪随机数，我们需要对产生随机数的种子进行不断的重播，从而达到我们实际需求的随机数效果。我们可以通过 srand() 函数来重新“播种”，这样种子就会发生改变。
* 第35堂课示例：随机数
* 郑凯
* 2020年5月25日
* */
#include <stdio.h>
#include <stdlib.h>
int main()
{
int rands;
rands = rand();
printf("rand number is %d\n", rands);
printf("rand number2 is %d\n", rand());
return 0;
}
srand() 的用法为：
void srand (unsigned int seed);
它需要一个 unsigned int 类型的参数。在实际开发中，我们可以用时间作为参数，只要每次播种的时间不同，那么生成的种子就不同，最终的随机数也就不同，通常我们采用 <time.h> 头文件中的 time() 函数即可得到当前的时间【精准到秒】srand((unsigned)time(NULL));
/**小提示：根据种子与随机数的符合高斯分布的关系可知，生成的随机数是逐渐增大或者逐渐减小！
* 第35堂课示例：随机数
* 郑凯
* 2020年5月25日
* */
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
int main()
{
int rands;
srand((unsigned)time(NULL));
rands = rand();
printf("rand number is %d\n", rands);
printf("rand number2 is %d\n", rand());
return 0;
}
生成一定范围随机数
在实际编程开发中，实际需求往往是一定范围内的随机数，对于产生一定范围的随机数，就需要使用一定的技巧了，常用的方法是取模运算，再加上一个加法运算：
int a = rand() % 10; //产生0~9的随机数，注意10会被整除
如果要规定上下限：
int a = rand() % 51 + 100; //产生100~150的随机数
分析：取模即取余，rand()%51+13，看成两部分：rand()%51是产生 0~50 的随机数，后面+100保证 a 最小只能是 100，最大就是 50+100=150。
/**
* 第35堂课示例：有区间的随机数
* 例如：100~150之间的数字
* 郑凯
* 2020年5月25日
* */
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
int main()
{
int rands;
srand((unsigned)time(NULL));
rands = rand() % 51 + 100;
printf("rand number is %d\n", rands);
return 0;
}
根据种子与随机数的符合高斯分布的关系可知，生成的随机数是逐渐增大或者逐渐减小。
#2020学习打卡##C程序设计语言# C语言位字段的含义和用途
zkbhj 发表了文章 • 0 个评论 • 1521 次浏览 • 2020-05-14 16:34
存储空间很宝贵的情况下，可以考虑利用C语言位字段将多个数据保存在一个机器字。机器字指计算机一次能处理数据的bit位数，一般所说的32位系统即指其机器字长为32bit。
1.定义位字段：C语言位字段定义方法：
struct {
unsigned int a : 1; //冒号“:”后的数字为该位字段所占的bit位数
unsigned int b : 3;
unsigned int c : 5;
}flags;上面定义了一个flags变量，包含a,b,c三个位字段。位字段只能定义为以下3中类型：
1.int
2.signed int
3.unsigned int
需要提醒的是，位字段的赋值要特别小心范围，如unsigned int型flags.b只占3个位数，范围在000-111即0-7，超出范围会出现不可预知错误。
2.位字段访问：
1.位字段通过“.”号访问：flags.a , flags.b等等。
2.位字段没有独立的地址，不能进行取址操作。
3.位字段没有独立的存储空间，不能进行sizeof()操作。
3.内存分配规则：
1.位字段按声明顺序在机器字内存储
2.位字段不能跨越机器字存储，上一个机器字空间不足时，该位字段将全部存到下一个机器字
4.无名字段与0字段： struct {
unsigned int a : 1;
unsigned int : 3; //无名字段，不可访问，仅起占位作用
unsigned int : 0; //0字段，下一个位字段在新机器字边界
unsigned int b : 7;
}flags;
受0字段作用， 位字段flags.b将在下一个机器字边界开始存储。
查看全部
1.定义位字段：C语言位字段定义方法：
struct {
unsigned int a : 1; //冒号“:”后的数字为该位字段所占的bit位数
unsigned int b : 3;
unsigned int c : 5;
}flags;上面定义了一个flags变量，包含a,b,c三个位字段。位字段只能定义为以下3中类型：
1.int
2.signed int
3.unsigned int
需要提醒的是，位字段的赋值要特别小心范围，如unsigned int型flags.b只占3个位数，范围在000-111即0-7，超出范围会出现不可预知错误。
2.位字段访问：
1.位字段通过“.”号访问：flags.a , flags.b等等。
2.位字段没有独立的地址，不能进行取址操作。
3.位字段没有独立的存储空间，不能进行sizeof()操作。
3.内存分配规则：
1.位字段按声明顺序在机器字内存储
2.位字段不能跨越机器字存储，上一个机器字空间不足时，该位字段将全部存到下一个机器字
4.无名字段与0字段： struct {
unsigned int a : 1;
unsigned int : 3; //无名字段，不可访问，仅起占位作用
unsigned int : 0; //0字段，下一个位字段在新机器字边界
unsigned int b : 7;
}flags;
受0字段作用， 位字段flags.b将在下一个机器字边界开始存储。
查看全部
存储空间很宝贵的情况下，可以考虑利用C语言位字段将多个数据保存在一个机器字。机器字指计算机一次能处理数据的bit位数，一般所说的32位系统即指其机器字长为32bit。
1.定义位字段：C语言位字段定义方法：
1.int
2.signed int
3.unsigned int
需要提醒的是，位字段的赋值要特别小心范围，如unsigned int型flags.b只占3个位数，范围在000-111即0-7，超出范围会出现不可预知错误。
2.位字段访问：
1.位字段通过“.”号访问：flags.a , flags.b等等。
2.位字段没有独立的地址，不能进行取址操作。
3.位字段没有独立的存储空间，不能进行sizeof()操作。
3.内存分配规则：
1.位字段按声明顺序在机器字内存储
2.位字段不能跨越机器字存储，上一个机器字空间不足时，该位字段将全部存到下一个机器字
4.无名字段与0字段：
受0字段作用， 位字段flags.b将在下一个机器字边界开始存储。
1.定义位字段：C语言位字段定义方法：
struct {
unsigned int a : 1; //冒号“:”后的数字为该位字段所占的bit位数
unsigned int b : 3;
unsigned int c : 5;
}flags;上面定义了一个flags变量，包含a,b,c三个位字段。位字段只能定义为以下3中类型：1.int
2.signed int
3.unsigned int
需要提醒的是，位字段的赋值要特别小心范围，如unsigned int型flags.b只占3个位数，范围在000-111即0-7，超出范围会出现不可预知错误。
2.位字段访问：
1.位字段通过“.”号访问：flags.a , flags.b等等。
2.位字段没有独立的地址，不能进行取址操作。
3.位字段没有独立的存储空间，不能进行sizeof()操作。
3.内存分配规则：
1.位字段按声明顺序在机器字内存储
2.位字段不能跨越机器字存储，上一个机器字空间不足时，该位字段将全部存到下一个机器字
4.无名字段与0字段：
struct {
unsigned int a : 1;
unsigned int : 3; //无名字段，不可访问，仅起占位作用
unsigned int : 0; //0字段，下一个位字段在新机器字边界
unsigned int b : 7;
}flags;受0字段作用， 位字段flags.b将在下一个机器字边界开始存储。
数据结构之：二叉树
zkbhj 发表了文章 • 0 个评论 • 1312 次浏览 • 2020-05-08 11:56
在讨论二叉树之前，先复习几个重点的概念定义~
结点（Node）
结点是数据结构中的基础，是构成复杂数据结构的基本组成单位。
树（Tree）
树（Tree）是n（n>=0)个结点的有限集。n=0时称为空树。在任意一颗非空树中：
1）有且仅有一个特定的称为根（Root）的结点；
2）当n>1时，其余结点可分为m(m>0)个互不相交的有限集T1、T2、......、Tn，其中每一个集合本身又是一棵树，并且称为根的子树。
此外，树的定义还需要强调以下两点：
1）n>0时根结点是唯一的，不可能存在多个根结点，数据结构中的树只能有一个根结点。
2）m>0时，子树的个数没有限制，但它们一定是互不相交的。
结点的度
结点拥有的子树数目称为结点的度。
结点关系
结点子树的根结点为该结点的孩子结点。相应该结点称为孩子结点的双亲结点。同一个双亲结点的孩子结点之间互称兄弟结点。
结点层次
从根开始定义起，根为第一层，根的孩子为第二层，以此类推。
树的深度
树中结点的最大层次数称为树的深度或高度。
概念复习完成之后，进入二叉树正题！
二叉树
定义
二叉树是n(n>=0)个结点的有限集合，该集合或者为空集（称为空二叉树），或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树组成。
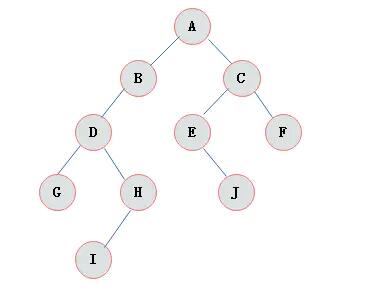
下图展示了一棵普通二叉树：
二叉树特点
由二叉树定义以及图示分析得出二叉树有以下特点：
1）每个结点最多有两颗子树，所以二叉树中不存在度大于2的结点。
2）左子树和右子树是有顺序的，次序不能任意颠倒。
3）即使树中某结点只有一棵子树，也要区分它是左子树还是右子树。
二叉树性质
1）在二叉树的第i层上最多有2i-1 个节点 。（i>=1）
2）二叉树中如果深度为k,那么最多有2k-1个节点。(k>=1）
3）n0=n2+1 n0表示度数为0的节点数，n2表示度数为2的节点数。
4）在完全二叉树中，具有n个节点的完全二叉树的深度为[log2n]+1，其中[log2n]是向下取整。
5）若对含 n 个结点的完全二叉树从上到下且从左至右进行 1 至 n 的编号，则对完全二叉树中任意一个编号为 i 的结点有如下特性：
(1) 若 i=1，则该结点是二叉树的根，无双亲, 否则，编号为 [i/2] 的结点为其双亲结点;
(2) 若 2i>n，则该结点无左孩子， 否则，编号为 2i 的结点为其左孩子结点；
(3) 若 2i+1>n，则该结点无右孩子结点， 否则，编号为2i+1 的结点为其右孩子结点。
作者：MrHorse1992
链接：https://www.jianshu.com/p/bf73c8d50dc2
来源：简书
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。 查看全部
结点（Node）
结点是数据结构中的基础，是构成复杂数据结构的基本组成单位。
树（Tree）
树（Tree）是n（n>=0)个结点的有限集。n=0时称为空树。在任意一颗非空树中：
1）有且仅有一个特定的称为根（Root）的结点；
2）当n>1时，其余结点可分为m(m>0)个互不相交的有限集T1、T2、......、Tn，其中每一个集合本身又是一棵树，并且称为根的子树。
此外，树的定义还需要强调以下两点：
1）n>0时根结点是唯一的，不可能存在多个根结点，数据结构中的树只能有一个根结点。
2）m>0时，子树的个数没有限制，但它们一定是互不相交的。
结点的度
结点拥有的子树数目称为结点的度。
结点关系
结点子树的根结点为该结点的孩子结点。相应该结点称为孩子结点的双亲结点。同一个双亲结点的孩子结点之间互称兄弟结点。
结点层次
从根开始定义起，根为第一层，根的孩子为第二层，以此类推。
树的深度
树中结点的最大层次数称为树的深度或高度。
概念复习完成之后，进入二叉树正题！
二叉树
定义
二叉树是n(n>=0)个结点的有限集合，该集合或者为空集（称为空二叉树），或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树组成。
下图展示了一棵普通二叉树：
二叉树特点
由二叉树定义以及图示分析得出二叉树有以下特点：
1）每个结点最多有两颗子树，所以二叉树中不存在度大于2的结点。
2）左子树和右子树是有顺序的，次序不能任意颠倒。
3）即使树中某结点只有一棵子树，也要区分它是左子树还是右子树。
二叉树性质
1）在二叉树的第i层上最多有2i-1 个节点 。（i>=1）
2）二叉树中如果深度为k,那么最多有2k-1个节点。(k>=1）
3）n0=n2+1 n0表示度数为0的节点数，n2表示度数为2的节点数。
4）在完全二叉树中，具有n个节点的完全二叉树的深度为[log2n]+1，其中[log2n]是向下取整。
5）若对含 n 个结点的完全二叉树从上到下且从左至右进行 1 至 n 的编号，则对完全二叉树中任意一个编号为 i 的结点有如下特性：
(1) 若 i=1，则该结点是二叉树的根，无双亲, 否则，编号为 [i/2] 的结点为其双亲结点;
(2) 若 2i>n，则该结点无左孩子， 否则，编号为 2i 的结点为其左孩子结点；
(3) 若 2i+1>n，则该结点无右孩子结点， 否则，编号为2i+1 的结点为其右孩子结点。
作者：MrHorse1992
链接：https://www.jianshu.com/p/bf73c8d50dc2
来源：简书
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。 查看全部
在讨论二叉树之前，先复习几个重点的概念定义~
结点（Node）
结点是数据结构中的基础，是构成复杂数据结构的基本组成单位。
树（Tree）
树（Tree）是n（n>=0)个结点的有限集。n=0时称为空树。在任意一颗非空树中：
1）有且仅有一个特定的称为根（Root）的结点；
2）当n>1时，其余结点可分为m(m>0)个互不相交的有限集T1、T2、......、Tn，其中每一个集合本身又是一棵树，并且称为根的子树。
此外，树的定义还需要强调以下两点：
1）n>0时根结点是唯一的，不可能存在多个根结点，数据结构中的树只能有一个根结点。
2）m>0时，子树的个数没有限制，但它们一定是互不相交的。
结点的度
结点拥有的子树数目称为结点的度。
结点关系
结点子树的根结点为该结点的孩子结点。相应该结点称为孩子结点的双亲结点。同一个双亲结点的孩子结点之间互称兄弟结点。
结点层次
从根开始定义起，根为第一层，根的孩子为第二层，以此类推。
树的深度
树中结点的最大层次数称为树的深度或高度。
概念复习完成之后，进入二叉树正题！
二叉树
定义
二叉树是n(n>=0)个结点的有限集合，该集合或者为空集（称为空二叉树），或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树组成。
下图展示了一棵普通二叉树：
二叉树特点
由二叉树定义以及图示分析得出二叉树有以下特点：
1）每个结点最多有两颗子树，所以二叉树中不存在度大于2的结点。
2）左子树和右子树是有顺序的，次序不能任意颠倒。
3）即使树中某结点只有一棵子树，也要区分它是左子树还是右子树。
二叉树性质
1）在二叉树的第i层上最多有2i-1 个节点 。（i>=1）
2）二叉树中如果深度为k,那么最多有2k-1个节点。(k>=1）
3）n0=n2+1 n0表示度数为0的节点数，n2表示度数为2的节点数。
4）在完全二叉树中，具有n个节点的完全二叉树的深度为[log2n]+1，其中[log2n]是向下取整。
5）若对含 n 个结点的完全二叉树从上到下且从左至右进行 1 至 n 的编号，则对完全二叉树中任意一个编号为 i 的结点有如下特性：
作者：MrHorse1992
链接：https://www.jianshu.com/p/bf73c8d50dc2
来源：简书
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
结点（Node）
结点是数据结构中的基础，是构成复杂数据结构的基本组成单位。
树（Tree）
树（Tree）是n（n>=0)个结点的有限集。n=0时称为空树。在任意一颗非空树中：
1）有且仅有一个特定的称为根（Root）的结点；
2）当n>1时，其余结点可分为m(m>0)个互不相交的有限集T1、T2、......、Tn，其中每一个集合本身又是一棵树，并且称为根的子树。
此外，树的定义还需要强调以下两点：
1）n>0时根结点是唯一的，不可能存在多个根结点，数据结构中的树只能有一个根结点。
2）m>0时，子树的个数没有限制，但它们一定是互不相交的。
结点的度
结点拥有的子树数目称为结点的度。
结点关系
结点子树的根结点为该结点的孩子结点。相应该结点称为孩子结点的双亲结点。同一个双亲结点的孩子结点之间互称兄弟结点。
结点层次
从根开始定义起，根为第一层，根的孩子为第二层，以此类推。
树的深度
树中结点的最大层次数称为树的深度或高度。
概念复习完成之后，进入二叉树正题！
二叉树
定义
二叉树是n(n>=0)个结点的有限集合，该集合或者为空集（称为空二叉树），或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树组成。
下图展示了一棵普通二叉树：
二叉树特点
由二叉树定义以及图示分析得出二叉树有以下特点：
1）每个结点最多有两颗子树，所以二叉树中不存在度大于2的结点。
2）左子树和右子树是有顺序的，次序不能任意颠倒。
3）即使树中某结点只有一棵子树，也要区分它是左子树还是右子树。
二叉树性质
1）在二叉树的第i层上最多有2i-1 个节点 。（i>=1）
2）二叉树中如果深度为k,那么最多有2k-1个节点。(k>=1）
3）n0=n2+1 n0表示度数为0的节点数，n2表示度数为2的节点数。
4）在完全二叉树中，具有n个节点的完全二叉树的深度为[log2n]+1，其中[log2n]是向下取整。
5）若对含 n 个结点的完全二叉树从上到下且从左至右进行 1 至 n 的编号，则对完全二叉树中任意一个编号为 i 的结点有如下特性：
(1) 若 i=1，则该结点是二叉树的根，无双亲, 否则，编号为 [i/2] 的结点为其双亲结点;
(2) 若 2i>n，则该结点无左孩子， 否则，编号为 2i 的结点为其左孩子结点；
(3) 若 2i+1>n，则该结点无右孩子结点， 否则，编号为2i+1 的结点为其右孩子结点。
作者：MrHorse1992
链接：https://www.jianshu.com/p/bf73c8d50dc2
来源：简书
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
#2020学习打卡##C程序设计语言# C语言实现快速排序
zkbhj 发表了文章 • 0 个评论 • 1263 次浏览 • 2020-04-23 17:24
关于什么是快速排序，可以参考文章 ：什么是快速排序。里面有介绍快速排序的方法以及和冒泡排序的区别，还有PHP版本实现快速排序的方法。本文章只讨论C语言实现的一种方式。#include <stdio.h>
//快速排序算法(从小到大)
//arr:需要排序的数组，begin:需要排序的区间左边界，end:需要排序的区间的右边界
void quickSort(int *arr,int begin,int end)
{
//如果区间不只一个数
if(begin < end)
{
int temp = arr[begin]; //将区间的第一个数作为基准数
int i = begin; //从左到右进行查找时的“指针”，指示当前左位置
int j = end; //从右到左进行查找时的“指针”，指示当前右位置
//不重复遍历
while(i < j)
{
//当右边的数大于基准数时，略过，继续向左查找
//不满足条件时跳出循环，此时的j对应的元素是小于基准元素的
while(i<j && arr[j] > temp)
j--;
//将右边小于等于基准元素的数填入右边相应位置
arr[i] = arr[j];
//当左边的数小于等于基准数时，略过，继续向右查找
//(重复的基准元素集合到左区间)
//不满足条件时跳出循环，此时的i对应的元素是大于等于基准元素的
while(i<j && arr[i] <= temp)
i++;
//将左边大于基准元素的数填入左边相应位置
arr[j] = arr[i];
}
//将基准元素填入相应位置
arr[i] = temp;
//此时的i即为基准元素的位置
//对基准元素的左边子区间进行相似的快速排序
quickSort(arr,begin,i-1);
//对基准元素的右边子区间进行相似的快速排序
quickSort(arr,i+1,end);
}
//如果区间只有一个数，则返回
else
return;
}
int main()
{
int num[12] = {23,45,17,11,13,89,72,26,3,17,11,13};
int n = 12;
quickSort(num,0,n-1);
printf("排序后的数组为：\n");
// for(int i=0;i<n;i++)
// printf("%d ", num[i]);
int *p = num;
while(n>0) {
n--;
printf("%d ",*p++);
}
return 0;
}
[/i][/i][/i][/i][/i][i][i][i][i]https://github.com/happy-hacki ... ort.c[/i][/i][/i][/i] 查看全部
//快速排序算法(从小到大)
//arr:需要排序的数组，begin:需要排序的区间左边界，end:需要排序的区间的右边界
void quickSort(int *arr,int begin,int end)
{
//如果区间不只一个数
if(begin < end)
{
int temp = arr[begin]; //将区间的第一个数作为基准数
int i = begin; //从左到右进行查找时的“指针”，指示当前左位置
int j = end; //从右到左进行查找时的“指针”，指示当前右位置
//不重复遍历
while(i < j)
{
//当右边的数大于基准数时，略过，继续向左查找
//不满足条件时跳出循环，此时的j对应的元素是小于基准元素的
while(i<j && arr[j] > temp)
j--;
//将右边小于等于基准元素的数填入右边相应位置
arr[i] = arr[j];
//当左边的数小于等于基准数时，略过，继续向右查找
//(重复的基准元素集合到左区间)
//不满足条件时跳出循环，此时的i对应的元素是大于等于基准元素的
while(i<j && arr[i] <= temp)
i++;
//将左边大于基准元素的数填入左边相应位置
arr[j] = arr[i];
}
//将基准元素填入相应位置
arr[i] = temp;
//此时的i即为基准元素的位置
//对基准元素的左边子区间进行相似的快速排序
quickSort(arr,begin,i-1);
//对基准元素的右边子区间进行相似的快速排序
quickSort(arr,i+1,end);
}
//如果区间只有一个数，则返回
else
return;
}
int main()
{
int num[12] = {23,45,17,11,13,89,72,26,3,17,11,13};
int n = 12;
quickSort(num,0,n-1);
printf("排序后的数组为：\n");
// for(int i=0;i<n;i++)
// printf("%d ", num[i]);
int *p = num;
while(n>0) {
n--;
printf("%d ",*p++);
}
return 0;
}
[/i][/i][/i][/i][/i][i][i][i][i]https://github.com/happy-hacki ... ort.c[/i][/i][/i][/i] 查看全部
关于什么是快速排序，可以参考文章 ：什么是快速排序。里面有介绍快速排序的方法以及和冒泡排序的区别，还有PHP版本实现快速排序的方法。本文章只讨论C语言实现的一种方式。
#include <stdio.h>[i][i][i][i]https://github.com/happy-hacki ... ort.c[/i][/i][/i][/i]
//快速排序算法(从小到大)
//arr:需要排序的数组，begin:需要排序的区间左边界，end:需要排序的区间的右边界
void quickSort(int *arr,int begin,int end)
{
//如果区间不只一个数
if(begin < end)
{
int temp = arr[begin]; //将区间的第一个数作为基准数
int i = begin; //从左到右进行查找时的“指针”，指示当前左位置
int j = end; //从右到左进行查找时的“指针”，指示当前右位置
//不重复遍历
while(i < j)
{
//当右边的数大于基准数时，略过，继续向左查找
//不满足条件时跳出循环，此时的j对应的元素是小于基准元素的
while(i<j && arr[j] > temp)
j--;
//将右边小于等于基准元素的数填入右边相应位置
arr[i] = arr[j];
//当左边的数小于等于基准数时，略过，继续向右查找
//(重复的基准元素集合到左区间)
//不满足条件时跳出循环，此时的i对应的元素是大于等于基准元素的
while(i<j && arr[i] <= temp)
i++;
//将左边大于基准元素的数填入左边相应位置
arr[j] = arr[i];
}
//将基准元素填入相应位置
arr[i] = temp;
//此时的i即为基准元素的位置
//对基准元素的左边子区间进行相似的快速排序
quickSort(arr,begin,i-1);
//对基准元素的右边子区间进行相似的快速排序
quickSort(arr,i+1,end);
}
//如果区间只有一个数，则返回
else
return;
}
int main()
{
int num[12] = {23,45,17,11,13,89,72,26,3,17,11,13};
int n = 12;
quickSort(num,0,n-1);
printf("排序后的数组为：\n");
// for(int i=0;i<n;i++)
// printf("%d ", num[i]);
int *p = num;
while(n>0) {
n--;
printf("%d ",*p++);
}
return 0;
}
[/i][/i][/i][/i][/i]
#2020学习打卡##C程序设计语言# 同样是字符串字面量赋值给指针变量*s和字符数组s[]有和区别？
zkbhj 发表了文章 • 0 个评论 • 1235 次浏览 • 2020-04-20 10:07
针对下面两种定义方式，会有什么不同？char s = "zkbhj";
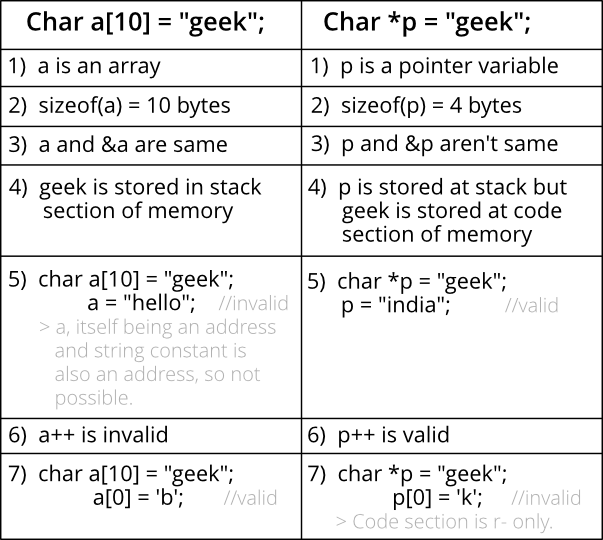
char *s = "zkbhj";
不同如下：
在声明时，char *s=“hello”声明了一个字符串常量，在使用时不能被修改；
在声明时，char s=“hello”声明了一个字符串变量，在使用时能被修改；
作为函数的形式参数时，char *s，char s没有区别
例如：f(char *s)等价于 f(char s)
参考文档：https://www.geeksforgeeks.org/ ... in-c/ 查看全部
char *s = "zkbhj";
不同如下：
在声明时，char *s=“hello”声明了一个字符串常量，在使用时不能被修改；
在声明时，char s=“hello”声明了一个字符串变量，在使用时能被修改；
作为函数的形式参数时，char *s，char s没有区别
例如：f(char *s)等价于 f(char s)
参考文档：https://www.geeksforgeeks.org/ ... in-c/ 查看全部
针对下面两种定义方式，会有什么不同？
不同如下：
例如：f(char *s)等价于 f(char s)
参考文档：https://www.geeksforgeeks.org/ ... in-c/
char s = "zkbhj";
char *s = "zkbhj";
不同如下：
在声明时，char *s=“hello”声明了一个字符串常量，在使用时不能被修改；
在声明时，char s=“hello”声明了一个字符串变量，在使用时能被修改；
作为函数的形式参数时，char *s，char s没有区别
例如：f(char *s)等价于 f(char s)
参考文档：https://www.geeksforgeeks.org/ ... in-c/
#2020学习打卡##C程序设计语言# 直接插入排序和改进版Shell排序解析
zkbhj 发表了文章 • 0 个评论 • 1177 次浏览 • 2020-04-14 17:54
一、直接插入排序
直接插入排序（Straight Insertion Sort）是一种最简单的排序方法，其基本操作是将一条记录插入到已排好的有序表中，从而得到一个新的、记录数量增1的有序表。直接插入排序的时间复杂度为 O(n2)。
实例如下所示：
定义的数组 ： {23,34,56,78,65,90,88,92,18,21}
过程如下所示：
【23】 34 56 78 65 90 88 92 18 21
第 1 次排序结果： 【23 34】 56 78 65 90 88 92 18 21
——用34插入到【23】序列中，34>23，故插入后的顺序是【23，34】
第 2 次排序结果： 【 23 34 56 】78 65 90 88 92 18 21
——用56插入到【23，34】序列中，56>34，故插入后的顺序是【23，34，56】
第 3 次排序结果： 【23 34 56 78】65 90 88 92 18 21
——用78插入到【23，34，56】序列中，78>56，故插入后的顺序是【23，34，56，78】
第 4 次排序结果： 【23 34 56 65 78 】90 88 92 18 21
——用65插入到【23，34，56，78】序列中，65<78，所以78后移一位，和56比较，65>56,故插入后的顺序是【23，34，56，65, 78】
第 5 次排序结果： 【23 34 56 65 78 90 】 88 92 18 21
——用90插入到【23，34，56，65, 78】序列中，78<90 ,故插入后的顺序是【23 34 56 65 78 90 】
第 6 次排序结果： 23 34 56 65 78 88 90 92 18 21
——用88插入到【23 34 56 65 78 90 】序列中，90>88 ,所以90后移一位,故插入后的顺序是【23 34 56 65 78 88 90】
第 7 次排序结果： 23 34 56 65 78 88 90 92 18 21
——用92插入到【23 34 56 65 78 90 】序列中，90<92 ,故插入后的顺序是【23 34 56 65 78 90 92 】
第 8 次排序结果： 18 23 34 56 65 78 88 90 92 21
——用18插入到【23 34 56 65 78 90 92 】序列中，18<92，所以92后移一位，和90比较，90>18,依次后移，直到第一位23，因为18<23, 故插入后的顺序是【18 23 34 56 65 78 88 90 92】
第 9 次排序结果： 18 21 23 34 56 65 78 88 90 92
——用21插入到【23 34 56 65 78 90 92 】序列中，21<92，故92后移一位，和90比较，90>21,依次后移，直到第一位18，因为18<21, 故插入后的顺序是【18 21 23 34 56 65 78 88 90 92】
C语言实现：#include <stdio.h>
//自定义的输出函数
void print(int a, int n ,int i){
printf("%d:",i);
for(int j=0; j<8; j++){
printf("%d",a[j]);
}
printf("\n");
}
//直接插入排序函数
void InsertSort(int a, int n)
{
for(int i= 1; i<n; i++){
if(a < a[i-1]){//若第 i 个元素大于 i-1 元素则直接插入；反之，需要找到适当的插入位置后在插入。
int j= i-1;
int x = a;
while(j>-1 && x < a[j]){ //采用顺序查找方式找到插入的位置，在查找的同时，将数组中的元素进行后移操作，给插入元素腾出空间
a[j+1] = a[j];
j--;
}
a[j+1] = x; //插入到正确位置
}
print(a,n,i);//打印每次排序后的结果
}
}
int main(){
int a[8] = {3,1,7,5,2,4,9,6};
InsertSort(a,8);
return 0;
}
二、Shell排序：直接插入排序算法的一种高速而稳定的改进版本
希尔排序，也称递减增量排序算法，是一种插入排序算法，它出自D.L.Shell，因此而得名。Shell排序又称作缩小增量排序。Shell排序的执行时间依赖于增量序列。
希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。
先取一个小于n的整数d1作为第一个增量，把文件的全部记录分组。所有距离为d1的倍数的记录放在同一个组中。先在各组内进行直接插入排序；然后，取第二个增量d2<d1重复上述的分组和排序，直至所取的增量=1(<…<d2<d1)，即所有记录放在同一组中进行直接插入排序为止。
Shell排序算法的特点
希尔排序是基于插入排序的以下两点性质而提出改进方法的：
插入排序在对几乎已经排好序的数据操作时， 效率高， 即可以达到线性排序的效率[list][*]但插入排序一般来说是低效的， 因为插入排序每次只能将数据移动一位
[/*]
[/list]
时间复杂度：最坏情况下为O(n^2)，平均时间复杂度为O(nlogn)；
空间复杂度：归并排序需要一个大小为1的临时存储空间用以保存合并序列，所以空间复杂度为O(1)
算法稳定性：从上面图片中可以看出，数字5在排序后交换了位置，所以它是不稳定的算法。
例如：12、5、9、34、6、8、33、56、89、0、7、4、22、55、77
具体步骤：
void Shell(int *arr,int len,int gap)
{
for(int i = gap;i < len;i++)
{
int temp = arr;
int j = 0;
for(j = i-gap;j >= 0;j-=gap)
{
if(arr[j] > temp)
{
arr[j+gap] = arr[j];
}
else
{
break;
}
}
arr[j+gap] = temp;
}
}
void Shell_Sort(int *arr,int len)
{
int drr = {5,3,1}; //drr为分的组数，这里5，3，1不固定，但必须相互为素数，且最后数为1
int lend = sizeof(drr)/sizeof(drr[0]);
for(int i = 0;i < lend;i++)
{
Shell(arr,len,drr);
}
}
引用文章：
https://blog.csdn.net/FDk_LCL/java/article/details/90581904
https://www.cnblogs.com/guopengxia0719/p/10520561.html
https://www.cnblogs.com/BaoZiY/p/10931406.html
查看全部
直接插入排序（Straight Insertion Sort）是一种最简单的排序方法，其基本操作是将一条记录插入到已排好的有序表中，从而得到一个新的、记录数量增1的有序表。直接插入排序的时间复杂度为 O(n2)。
实例如下所示：
定义的数组 ： {23,34,56,78,65,90,88,92,18,21}
过程如下所示：
【23】 34 56 78 65 90 88 92 18 21
第 1 次排序结果： 【23 34】 56 78 65 90 88 92 18 21
——用34插入到【23】序列中，34>23，故插入后的顺序是【23，34】
第 2 次排序结果： 【 23 34 56 】78 65 90 88 92 18 21
——用56插入到【23，34】序列中，56>34，故插入后的顺序是【23，34，56】
第 3 次排序结果： 【23 34 56 78】65 90 88 92 18 21
——用78插入到【23，34，56】序列中，78>56，故插入后的顺序是【23，34，56，78】
第 4 次排序结果： 【23 34 56 65 78 】90 88 92 18 21
——用65插入到【23，34，56，78】序列中，65<78，所以78后移一位，和56比较，65>56,故插入后的顺序是【23，34，56，65, 78】
第 5 次排序结果： 【23 34 56 65 78 90 】 88 92 18 21
——用90插入到【23，34，56，65, 78】序列中，78<90 ,故插入后的顺序是【23 34 56 65 78 90 】
第 6 次排序结果： 23 34 56 65 78 88 90 92 18 21
——用88插入到【23 34 56 65 78 90 】序列中，90>88 ,所以90后移一位,故插入后的顺序是【23 34 56 65 78 88 90】
第 7 次排序结果： 23 34 56 65 78 88 90 92 18 21
——用92插入到【23 34 56 65 78 90 】序列中，90<92 ,故插入后的顺序是【23 34 56 65 78 90 92 】
第 8 次排序结果： 18 23 34 56 65 78 88 90 92 21
——用18插入到【23 34 56 65 78 90 92 】序列中，18<92，所以92后移一位，和90比较，90>18,依次后移，直到第一位23，因为18<23, 故插入后的顺序是【18 23 34 56 65 78 88 90 92】
第 9 次排序结果： 18 21 23 34 56 65 78 88 90 92
——用21插入到【23 34 56 65 78 90 92 】序列中，21<92，故92后移一位，和90比较，90>21,依次后移，直到第一位18，因为18<21, 故插入后的顺序是【18 21 23 34 56 65 78 88 90 92】
C语言实现：#include <stdio.h>
//自定义的输出函数
void print(int a, int n ,int i){
printf("%d:",i);
for(int j=0; j<8; j++){
printf("%d",a[j]);
}
printf("\n");
}
//直接插入排序函数
void InsertSort(int a, int n)
{
for(int i= 1; i<n; i++){
if(a < a[i-1]){//若第 i 个元素大于 i-1 元素则直接插入；反之，需要找到适当的插入位置后在插入。
int j= i-1;
int x = a;
while(j>-1 && x < a[j]){ //采用顺序查找方式找到插入的位置，在查找的同时，将数组中的元素进行后移操作，给插入元素腾出空间
a[j+1] = a[j];
j--;
}
a[j+1] = x; //插入到正确位置
}
print(a,n,i);//打印每次排序后的结果
}
}
int main(){
int a[8] = {3,1,7,5,2,4,9,6};
InsertSort(a,8);
return 0;
}
二、Shell排序：直接插入排序算法的一种高速而稳定的改进版本
希尔排序，也称递减增量排序算法，是一种插入排序算法，它出自D.L.Shell，因此而得名。Shell排序又称作缩小增量排序。Shell排序的执行时间依赖于增量序列。
希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。
先取一个小于n的整数d1作为第一个增量，把文件的全部记录分组。所有距离为d1的倍数的记录放在同一个组中。先在各组内进行直接插入排序；然后，取第二个增量d2<d1重复上述的分组和排序，直至所取的增量=1(<…<d2<d1)，即所有记录放在同一组中进行直接插入排序为止。
Shell排序算法的特点
希尔排序是基于插入排序的以下两点性质而提出改进方法的：
插入排序在对几乎已经排好序的数据操作时， 效率高， 即可以达到线性排序的效率[list][*]但插入排序一般来说是低效的， 因为插入排序每次只能将数据移动一位
[/*]
[/list]
时间复杂度：最坏情况下为O(n^2)，平均时间复杂度为O(nlogn)；
空间复杂度：归并排序需要一个大小为1的临时存储空间用以保存合并序列，所以空间复杂度为O(1)
算法稳定性：从上面图片中可以看出，数字5在排序后交换了位置，所以它是不稳定的算法。
例如：12、5、9、34、6、8、33、56、89、0、7、4、22、55、77
具体步骤：
void Shell(int *arr,int len,int gap)
{
for(int i = gap;i < len;i++)
{
int temp = arr;
int j = 0;
for(j = i-gap;j >= 0;j-=gap)
{
if(arr[j] > temp)
{
arr[j+gap] = arr[j];
}
else
{
break;
}
}
arr[j+gap] = temp;
}
}
void Shell_Sort(int *arr,int len)
{
int drr = {5,3,1}; //drr为分的组数，这里5，3，1不固定，但必须相互为素数，且最后数为1
int lend = sizeof(drr)/sizeof(drr[0]);
for(int i = 0;i < lend;i++)
{
Shell(arr,len,drr);
}
}
引用文章：
https://blog.csdn.net/FDk_LCL/java/article/details/90581904
https://www.cnblogs.com/guopengxia0719/p/10520561.html
https://www.cnblogs.com/BaoZiY/p/10931406.html
查看全部
一、直接插入排序
实例如下所示：
定义的数组 ： {23,34,56,78,65,90,88,92,18,21}
过程如下所示：
【23】 34 56 78 65 90 88 92 18 21
第 1 次排序结果： 【23 34】 56 78 65 90 88 92 18 21
——用34插入到【23】序列中，34>23，故插入后的顺序是【23，34】
第 2 次排序结果： 【 23 34 56 】78 65 90 88 92 18 21
——用56插入到【23，34】序列中，56>34，故插入后的顺序是【23，34，56】
第 3 次排序结果： 【23 34 56 78】65 90 88 92 18 21
——用78插入到【23，34，56】序列中，78>56，故插入后的顺序是【23，34，56，78】
第 4 次排序结果： 【23 34 56 65 78 】90 88 92 18 21
——用65插入到【23，34，56，78】序列中，65<78，所以78后移一位，和56比较，65>56,故插入后的顺序是【23，34，56，65, 78】
第 5 次排序结果： 【23 34 56 65 78 90 】 88 92 18 21
——用90插入到【23，34，56，65, 78】序列中，78<90 ,故插入后的顺序是【23 34 56 65 78 90 】
第 6 次排序结果： 23 34 56 65 78 88 90 92 18 21
——用88插入到【23 34 56 65 78 90 】序列中，90>88 ,所以90后移一位,故插入后的顺序是【23 34 56 65 78 88 90】
第 7 次排序结果： 23 34 56 65 78 88 90 92 18 21
——用92插入到【23 34 56 65 78 90 】序列中，90<92 ,故插入后的顺序是【23 34 56 65 78 90 92 】
第 8 次排序结果： 18 23 34 56 65 78 88 90 92 21
——用18插入到【23 34 56 65 78 90 92 】序列中，18<92，所以92后移一位，和90比较，90>18,依次后移，直到第一位23，因为18<23, 故插入后的顺序是【18 23 34 56 65 78 88 90 92】
第 9 次排序结果： 18 21 23 34 56 65 78 88 90 92
——用21插入到【23 34 56 65 78 90 92 】序列中，21<92，故92后移一位，和90比较，90>21,依次后移，直到第一位18，因为18<21, 故插入后的顺序是【18 21 23 34 56 65 78 88 90 92】
C语言实现：
二、Shell排序：直接插入排序算法的一种高速而稳定的改进版本
希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。
先取一个小于n的整数d1作为第一个增量，把文件的全部记录分组。所有距离为d1的倍数的记录放在同一个组中。先在各组内进行直接插入排序；然后，取第二个增量d2<d1重复上述的分组和排序，直至所取的增量=1(<…<d2<d1)，即所有记录放在同一组中进行直接插入排序为止。
Shell排序算法的特点
例如：12、5、9、34、6、8、33、56、89、0、7、4、22、55、77
具体步骤：
引用文章：
https://blog.csdn.net/FDk_LCL/java/article/details/90581904
https://www.cnblogs.com/guopengxia0719/p/10520561.html
https://www.cnblogs.com/BaoZiY/p/10931406.html
直接插入排序（Straight Insertion Sort）是一种最简单的排序方法，其基本操作是将一条记录插入到已排好的有序表中，从而得到一个新的、记录数量增1的有序表。直接插入排序的时间复杂度为 O(n2)。
实例如下所示：
定义的数组 ： {23,34,56,78,65,90,88,92,18,21}
过程如下所示：
【23】 34 56 78 65 90 88 92 18 21
第 1 次排序结果： 【23 34】 56 78 65 90 88 92 18 21
——用34插入到【23】序列中，34>23，故插入后的顺序是【23，34】
第 2 次排序结果： 【 23 34 56 】78 65 90 88 92 18 21
——用56插入到【23，34】序列中，56>34，故插入后的顺序是【23，34，56】
第 3 次排序结果： 【23 34 56 78】65 90 88 92 18 21
——用78插入到【23，34，56】序列中，78>56，故插入后的顺序是【23，34，56，78】
第 4 次排序结果： 【23 34 56 65 78 】90 88 92 18 21
——用65插入到【23，34，56，78】序列中，65<78，所以78后移一位，和56比较，65>56,故插入后的顺序是【23，34，56，65, 78】
第 5 次排序结果： 【23 34 56 65 78 90 】 88 92 18 21
——用90插入到【23，34，56，65, 78】序列中，78<90 ,故插入后的顺序是【23 34 56 65 78 90 】
第 6 次排序结果： 23 34 56 65 78 88 90 92 18 21
——用88插入到【23 34 56 65 78 90 】序列中，90>88 ,所以90后移一位,故插入后的顺序是【23 34 56 65 78 88 90】
第 7 次排序结果： 23 34 56 65 78 88 90 92 18 21
——用92插入到【23 34 56 65 78 90 】序列中，90<92 ,故插入后的顺序是【23 34 56 65 78 90 92 】
第 8 次排序结果： 18 23 34 56 65 78 88 90 92 21
——用18插入到【23 34 56 65 78 90 92 】序列中，18<92，所以92后移一位，和90比较，90>18,依次后移，直到第一位23，因为18<23, 故插入后的顺序是【18 23 34 56 65 78 88 90 92】
第 9 次排序结果： 18 21 23 34 56 65 78 88 90 92
——用21插入到【23 34 56 65 78 90 92 】序列中，21<92，故92后移一位，和90比较，90>21,依次后移，直到第一位18，因为18<21, 故插入后的顺序是【18 21 23 34 56 65 78 88 90 92】
C语言实现：
#include <stdio.h>
//自定义的输出函数
void print(int a, int n ,int i){
printf("%d:",i);
for(int j=0; j<8; j++){
printf("%d",a[j]);
}
printf("\n");
}
//直接插入排序函数
void InsertSort(int a, int n)
{
for(int i= 1; i<n; i++){
if(a < a[i-1]){//若第 i 个元素大于 i-1 元素则直接插入；反之，需要找到适当的插入位置后在插入。
int j= i-1;
int x = a;
while(j>-1 && x < a[j]){ //采用顺序查找方式找到插入的位置，在查找的同时，将数组中的元素进行后移操作，给插入元素腾出空间
a[j+1] = a[j];
j--;
}
a[j+1] = x; //插入到正确位置
}
print(a,n,i);//打印每次排序后的结果
}
}
int main(){
int a[8] = {3,1,7,5,2,4,9,6};
InsertSort(a,8);
return 0;
}
二、Shell排序：直接插入排序算法的一种高速而稳定的改进版本
希尔排序，也称递减增量排序算法，是一种插入排序算法，它出自D.L.Shell，因此而得名。Shell排序又称作缩小增量排序。Shell排序的执行时间依赖于增量序列。
希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。
先取一个小于n的整数d1作为第一个增量，把文件的全部记录分组。所有距离为d1的倍数的记录放在同一个组中。先在各组内进行直接插入排序；然后，取第二个增量d2<d1重复上述的分组和排序，直至所取的增量=1(<…<d2<d1)，即所有记录放在同一组中进行直接插入排序为止。
Shell排序算法的特点
希尔排序是基于插入排序的以下两点性质而提出改进方法的：
- 插入排序在对几乎已经排好序的数据操作时， 效率高， 即可以达到线性排序的效率[list][*]但插入排序一般来说是低效的， 因为插入排序每次只能将数据移动一位
[/*]
[/list]
时间复杂度：最坏情况下为O(n^2)，平均时间复杂度为O(nlogn)；
空间复杂度：归并排序需要一个大小为1的临时存储空间用以保存合并序列，所以空间复杂度为O(1)
算法稳定性：从上面图片中可以看出，数字5在排序后交换了位置，所以它是不稳定的算法。
例如：12、5、9、34、6、8、33、56、89、0、7、4、22、55、77
具体步骤：
void Shell(int *arr,int len,int gap)
{
for(int i = gap;i < len;i++)
{
int temp = arr;
int j = 0;
for(j = i-gap;j >= 0;j-=gap)
{
if(arr[j] > temp)
{
arr[j+gap] = arr[j];
}
else
{
break;
}
}
arr[j+gap] = temp;
}
}
void Shell_Sort(int *arr,int len)
{
int drr = {5,3,1}; //drr为分的组数，这里5，3，1不固定，但必须相互为素数，且最后数为1
int lend = sizeof(drr)/sizeof(drr[0]);
for(int i = 0;i < lend;i++)
{
Shell(arr,len,drr);
}
}
引用文章：
https://blog.csdn.net/FDk_LCL/java/article/details/90581904
https://www.cnblogs.com/guopengxia0719/p/10520561.html
https://www.cnblogs.com/BaoZiY/p/10931406.html
#2020学习打卡##C程序设计语言# 为什么C教材和程序里有时候要使用八进制或者十六进制的数字形式呢？
回复zkbhj 发起了问题 • 1 人关注 • 0 个回复 • 2183 次浏览 • 2020-04-12 23:56
#2020学习打卡##C程序设计语言# 各种字符编码都有什么区别和联系？
zkbhj 发表了文章 • 0 个评论 • 1198 次浏览 • 2020-04-09 12:02
今天在学习C语言的过程中，第一次接触到一个字符编码“EBCDIC”，它又和我们已经知道过的 ASCII，Unicode有哪些区别和联系呢？
一、EBCDIC
EBCDIC (Extended Binary Coded Decimal Interchange Code) 为国际商用机器公司(IBM)于1963年-64年间推出的字符编码表，根据早期打孔机式的二进化十进数(BCD, Binary Coded Decimal)排列而成。，是IBM为它的更大型的操作系统而开发的。
EBCDIC编码中，英文字母不是连续地排列，中间出现多次断续，为撰写程序的人带来了一些困难。
ASCII比EBCDIC后出现，ASCII的编码方式参照了EBCDIC，将英文连了起来，方便了程序员记忆。因此，就连IBM的个人计算机和工作站操作系统也不使用它们所有的EBCDIC编码。相反的，它们使用文本的工业标准编码，ASCII码。
转化程序允许不同的操作系统从一种编码到另一种编码的转化。
二、ASCII
ASCII ((American Standard Code for Information Interchange): 美国信息交换标准代码）是基于拉丁字母的一套电脑编码系统，主要用于显示现代英语和其他西欧语言。它是最通用的信息交换标准，并等同于国际标准ISO/IEC 646。ASCII第一次以规范标准的类型发表是在1967年，最后一次更新则是在1986年，到目前为止共定义了128个字符。
三、Unicode
Unicode（统一码、万国码、单一码）是计算机科学领域里的一项业界标准，包括字符集、编码方案等。Unicode 是为了解决传统的字符编码方案的局限而产生的，它为每种语言中的每个字符设定了统一并且唯一的二进制编码，以满足跨语言、跨平台进行文本转换、处理的要求。1990年开始研发，1994年正式公布。
Unicode是国际组织制定的可以容纳世界上所有文字和符号的字符编码方案。目前的Unicode字符分为17组编排，0x0000 至 0x10FFFF，每组称为平面（Plane），而每平面拥有65536个码位，共1114112个。然而目前只用了少数平面。UTF-8、UTF-16、UTF-32都是将数字转换到程序数据的编码方案。
四、更多
目前的文字编码标准主要有 ASCII、GB2312、GBK、Unicode等。ASCII 编码是最简单的西文编码方案。GB2312、GBK、GB18030 是汉字字符编码方案的国家标准。ISO/IEC 10646 和 Unicode 都是全球字符编码的国际标准。 查看全部
一、EBCDIC
EBCDIC (Extended Binary Coded Decimal Interchange Code) 为国际商用机器公司(IBM)于1963年-64年间推出的字符编码表，根据早期打孔机式的二进化十进数(BCD, Binary Coded Decimal)排列而成。，是IBM为它的更大型的操作系统而开发的。
EBCDIC编码中，英文字母不是连续地排列，中间出现多次断续，为撰写程序的人带来了一些困难。
ASCII比EBCDIC后出现，ASCII的编码方式参照了EBCDIC，将英文连了起来，方便了程序员记忆。因此，就连IBM的个人计算机和工作站操作系统也不使用它们所有的EBCDIC编码。相反的，它们使用文本的工业标准编码，ASCII码。
转化程序允许不同的操作系统从一种编码到另一种编码的转化。
二、ASCII
ASCII ((American Standard Code for Information Interchange): 美国信息交换标准代码）是基于拉丁字母的一套电脑编码系统，主要用于显示现代英语和其他西欧语言。它是最通用的信息交换标准，并等同于国际标准ISO/IEC 646。ASCII第一次以规范标准的类型发表是在1967年，最后一次更新则是在1986年，到目前为止共定义了128个字符。
三、Unicode
Unicode（统一码、万国码、单一码）是计算机科学领域里的一项业界标准，包括字符集、编码方案等。Unicode 是为了解决传统的字符编码方案的局限而产生的，它为每种语言中的每个字符设定了统一并且唯一的二进制编码，以满足跨语言、跨平台进行文本转换、处理的要求。1990年开始研发，1994年正式公布。
Unicode是国际组织制定的可以容纳世界上所有文字和符号的字符编码方案。目前的Unicode字符分为17组编排，0x0000 至 0x10FFFF，每组称为平面（Plane），而每平面拥有65536个码位，共1114112个。然而目前只用了少数平面。UTF-8、UTF-16、UTF-32都是将数字转换到程序数据的编码方案。
四、更多
目前的文字编码标准主要有 ASCII、GB2312、GBK、Unicode等。ASCII 编码是最简单的西文编码方案。GB2312、GBK、GB18030 是汉字字符编码方案的国家标准。ISO/IEC 10646 和 Unicode 都是全球字符编码的国际标准。 查看全部
今天在学习C语言的过程中，第一次接触到一个字符编码“EBCDIC”，它又和我们已经知道过的 ASCII，Unicode有哪些区别和联系呢？
一、EBCDIC
EBCDIC编码中，英文字母不是连续地排列，中间出现多次断续，为撰写程序的人带来了一些困难。
ASCII比EBCDIC后出现，ASCII的编码方式参照了EBCDIC，将英文连了起来，方便了程序员记忆。因此，就连IBM的个人计算机和工作站操作系统也不使用它们所有的EBCDIC编码。相反的，它们使用文本的工业标准编码，ASCII码。
转化程序允许不同的操作系统从一种编码到另一种编码的转化。
二、ASCII
三、Unicode
Unicode是国际组织制定的可以容纳世界上所有文字和符号的字符编码方案。目前的Unicode字符分为17组编排，0x0000 至 0x10FFFF，每组称为平面（Plane），而每平面拥有65536个码位，共1114112个。然而目前只用了少数平面。UTF-8、UTF-16、UTF-32都是将数字转换到程序数据的编码方案。
四、更多
目前的文字编码标准主要有 ASCII、GB2312、GBK、Unicode等。ASCII 编码是最简单的西文编码方案。GB2312、GBK、GB18030 是汉字字符编码方案的国家标准。ISO/IEC 10646 和 Unicode 都是全球字符编码的国际标准。
一、EBCDIC
EBCDIC (Extended Binary Coded Decimal Interchange Code) 为国际商用机器公司(IBM)于1963年-64年间推出的字符编码表，根据早期打孔机式的二进化十进数(BCD, Binary Coded Decimal)排列而成。，是IBM为它的更大型的操作系统而开发的。
EBCDIC编码中，英文字母不是连续地排列，中间出现多次断续，为撰写程序的人带来了一些困难。
ASCII比EBCDIC后出现，ASCII的编码方式参照了EBCDIC，将英文连了起来，方便了程序员记忆。因此，就连IBM的个人计算机和工作站操作系统也不使用它们所有的EBCDIC编码。相反的，它们使用文本的工业标准编码，ASCII码。
转化程序允许不同的操作系统从一种编码到另一种编码的转化。
二、ASCII
ASCII ((American Standard Code for Information Interchange): 美国信息交换标准代码）是基于拉丁字母的一套电脑编码系统，主要用于显示现代英语和其他西欧语言。它是最通用的信息交换标准，并等同于国际标准ISO/IEC 646。ASCII第一次以规范标准的类型发表是在1967年，最后一次更新则是在1986年，到目前为止共定义了128个字符。
三、Unicode
Unicode（统一码、万国码、单一码）是计算机科学领域里的一项业界标准，包括字符集、编码方案等。Unicode 是为了解决传统的字符编码方案的局限而产生的，它为每种语言中的每个字符设定了统一并且唯一的二进制编码，以满足跨语言、跨平台进行文本转换、处理的要求。1990年开始研发，1994年正式公布。
Unicode是国际组织制定的可以容纳世界上所有文字和符号的字符编码方案。目前的Unicode字符分为17组编排，0x0000 至 0x10FFFF，每组称为平面（Plane），而每平面拥有65536个码位，共1114112个。然而目前只用了少数平面。UTF-8、UTF-16、UTF-32都是将数字转换到程序数据的编码方案。
四、更多
目前的文字编码标准主要有 ASCII、GB2312、GBK、Unicode等。ASCII 编码是最简单的西文编码方案。GB2312、GBK、GB18030 是汉字字符编码方案的国家标准。ISO/IEC 10646 和 Unicode 都是全球字符编码的国际标准。
#2020学习打卡##C程序设计语言# Long类型在windows和Mac(类unix)系统下的差异分析
zkbhj 发表了文章 • 0 个评论 • 1377 次浏览 • 2020-04-08 11:36
在今天的课堂任务中，相同的程序代码，在windows和Mac os两个平台下，编译执行之后的结果竟然不太一样，有点儿“奇怪”，想知道原因为何？所以进行了一番研究梳理！
首先看下代码源码：很简单，要求就是通过标准文件中定义的常量 和 计算 两种方式来显示各数据类型的实际取值范围。#include <stdio.h>
#include <limits.h>
#include <float.h>
int main()
{
//从标准头文件中输出
printf("The values from standard file:\n");
printf("------------------------------\n");
printf("signed char: %d ~ %d\n",SCHAR_MIN , SCHAR_MAX);
printf("unSigned char: %d ~ %u\n",0 , UCHAR_MAX);
printf("signed short: %d ~ %d\n",SHRT_MIN, SHRT_MAX);
printf("unSigned short: %d ~ %u\n",0 , UCHAR_MAX);
printf("signed int: %d ~ %d\n",INT_MIN, INT_MAX);
printf("unSigned int: %d ~ %u\n",0 , UCHAR_MAX);
printf("signed long: %ld ~ %ld\n",LONG_MIN , LONG_MAX);
printf("unSigned long: %d ~ %lu\n",0 , ULONG_MAX);
printf("------------------------------\n");
//直接计算
printf("The values from calculate:\n");
printf("------------------------------\n");
printf("signed char: %d ~ %d\n", -(char)((unsigned char) ~0 >> 1) - 1, (char)((unsigned char) ~0 >> 1));
printf("unSigned char: %d ~ %u\n",0 , (unsigned char) ~0);
printf("signed short: %d ~ %d\n",-(short)((unsigned short) ~0 >> 1) - 1, (short)((unsigned short) ~0 >> 1));
printf("unSigned short: %d ~ %u\n",0 , (unsigned short) ~0);
printf("signed int: %d ~ %d\n",-(int)((unsigned int) ~0 >> 1) - 1, (int)((unsigned int) ~0 >> 1));
printf("unSigned int: %d ~ %u\n",0 ,(unsigned int) ~0);
printf("signed long: %ld ~ %ld\n",-(long)((unsigned long) ~0 >> 1) - 1, (long)((unsigned long) ~0 >> 1));
printf("unSigned long: %d ~ %lu\n",0 ,(unsigned long) ~0);
//查看类型占用字节数
long long a;
printf("%ld", sizeof a);
return 0;
}#操作系统的情况
Windows 10 64位系统
Mac OS 64位系统
可以看到，char、short、int这三个类型的数据长度，在两个平台下的长度是一致的，但是long类型就不太一样了，明显mac上的取值范围更大，而且大很多~ 为什么呢？
我们都知道，类型的取值范围是多少，取决于其所占用的位数，那么两个平台，针对long类型，显然分配的位数是不同的。通过sizeof（对这个详细了解再总结吧），总之它是C/C++中的一个操作符（operator），简单的说其作用就是返回一个对象或者类型所占的内存字节数。所以，在程序中加入了下面的代码，查看下两个系统中long分别分配的内存字节数，就可以知道对应的位数了。
//查看类型占用字节数
long a;
printf("%ld", sizeof a);果然，在Windows下，输出结果是4，在mac下输出结果是8。换算成位数，也就是windows下是32位，mac下是64位。这就解释了为啥两个系统下的long类型取值范围为啥不相同了。
但是另外一个问题来了：为啥同样是64位系统，window下long就是32位，而Mac下是64位呢？经过查询资料，才发现其中的门道。
在Unix世界中，针对64位平台的整数和指针的大小有一些可能的安排。其中最常用的两个是ILP64（实际上，这只是其中的一小部分例子，Cray就是这样）和LP64（几乎所有其他的）。首字母来自'int，long，指针是64位'和'long，指针是64位'。
Type ILP64 LP64 LLP64
char 8 8 8
short 16 16 16
int 64 32 32
long 64 64 32
long long 64 64 64
pointer 64 64 64ILP64系统因LP64而被放弃（也就是说，几乎所有后来的进入者都使用LP64，这是基于Aspen小组的建议;只有具有64位操作悠久遗产的系统使用不同的方案）。所有现代的64位Unix系统都使用LP64。MacOS X和Linux都是现代64位系统。
Microsoft使用不同的方案转换为64位：LLP64（'long long，指针为64位'）。这意味着32位软件可以在不改变的情况下重新编译。它具有与其他人不同的缺点，还需要对代码进行修改以利用64位容量。总是需要修改; 它只是与Unix平台上需要的版本不同的修订版本。
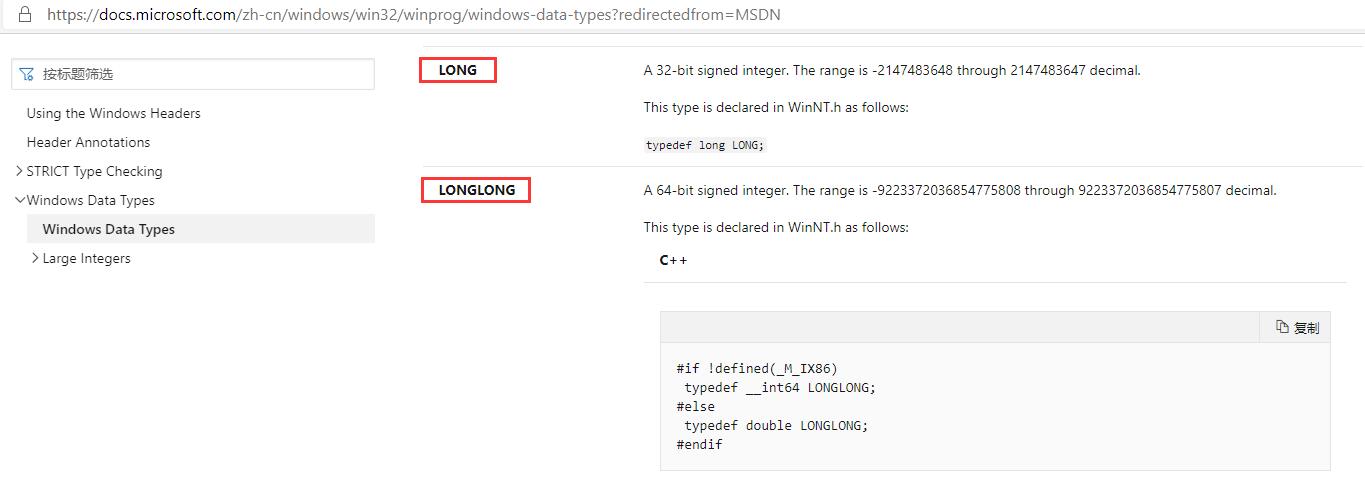
这下可以解释了，为什么windows下的long类型是32位的，因为Microsoft针对64位系统，采用的是LLP64位的方案。在这方案里，long类型是32位，longlong类型才是64位。在windows的官方说明文档中，也可以查到相应的类型释义：
那么，我们把程序改一改，是不是就可以输出相同的结果了呢？答案，不置可否！修改后的程序如下：#include <stdio.h>
#include <limits.h>
#include <float.h>
int main()
{
//从标准头文件中输出
printf("The values from standard file:\n");
printf("------------------------------\n");
printf("signed char: %d ~ %d\n",SCHAR_MIN , SCHAR_MAX);
printf("unSigned char: %d ~ %u\n",0 , UCHAR_MAX);
printf("signed short: %d ~ %d\n",SHRT_MIN, SHRT_MAX);
printf("unSigned short: %d ~ %u\n",0 , UCHAR_MAX);
printf("signed int: %d ~ %d\n",INT_MIN, INT_MAX);
printf("unSigned int: %d ~ %u\n",0 , UCHAR_MAX);
printf("signed long: %lld ~ %lld\n",LONG_LONG_MIN , LONG_LONG_MAX);
printf("unSigned long: %d ~ %llu\n",0 , ULLONG_MAX);
printf("------------------------------\n");
//直接计算
printf("The values from calculate:\n");
printf("------------------------------\n");
printf("signed char: %d ~ %d\n", -(char)((unsigned char) ~0 >> 1) - 1, (char)((unsigned char) ~0 >> 1));
printf("unSigned char: %d ~ %u\n",0 , (unsigned char) ~0);
printf("signed short: %d ~ %d\n",-(short)((unsigned short) ~0 >> 1) - 1, (short)((unsigned short) ~0 >> 1));
printf("unSigned short: %d ~ %u\n",0 , (unsigned short) ~0);
printf("signed int: %d ~ %d\n",-(int)((unsigned int) ~0 >> 1) - 1, (int)((unsigned int) ~0 >> 1));
printf("unSigned int: %d ~ %u\n",0 ,(unsigned int) ~0);
printf("signed long: %lld ~ %lld\n",-(long long)((unsigned long long) ~0 >> 1) - 1, (long long)((unsigned long long) ~0 >> 1));
printf("unSigned long: %d ~ %llu\n",0 ,(unsigned long long) ~0);
//查看类型占用字节数
long long a;
printf("%ld", sizeof a);
return 0;
}主要看long类型，我们替换成了long long，它对应的头文件常量是：LONG_LONG_MIN、LONG_LONG_MAX和ULLONG_MAX。当然，输出这个长度的数据，要使用 %lld 和 %llu。否则数据输出会变小。
题外话：
首先要说的是，和Java等语言不同，C/C++本身并没有规定各数据类型的位数，只是限定了一个大小关系，也就是规定从所占的bit数来说，short <= int <= long <= long long。至于具体哪种类型占用多少位，是由你所用的开发平台的编译器决定的。在现在的PC上一个通常的标准是，int和long同为32位，long long为64位。但是如果换到其它平台(如ARM)上，这个数字可能会有不同，类型所占的大小可以用sizeof()运算符查看。
long long是C99标准中新引进的数据类型，在古老的VC6.0中并没有这个类型，所以在VC6.0中用”long long”会发生编译错误。为了表示64位整数，VC6里采用的是微软自己搞出来的一个数据类型，叫做__int64，所以如果你是在VC6.0下编译的话，应该用__int64定义64位整型。新版的Visual Studio已经支持long long了。GCC是支持long long的，我们在win系统中使用的其它IDE如Dev-Cpp, Code::Blocks等等大多是采用的MinGW编译环境，它是与GCC兼容的，所以也支持long long（另外为了与MS兼容，也支持__int64）。如果是在纯的linux下，就只能使用long long了。
关于使用printf的输入输出，这里就有一个更囧的情况。实际上只要记住，主要的区分在于操作系统：如果在win系统下，那么无论什么编译器，一律用%I64d；如果在linux系统，一律用%lld。这是因为MS提供的msvcrt.dll库里使用的就是%I64d的方式，尽管Dev-Cpp等在语法上支持标准，但也不得不使用MS提供的dll库来完成IO，所以就造成了这种情况。
参考文档：
https://docs.microsoft.com/zh-cn/windows/win32/winprog/windows-data-types
https://cloud.tencent.com/developer/ask/62686
https://blog.csdn.net/qq_31736627/article/details/52912691
查看全部
首先看下代码源码：很简单，要求就是通过标准文件中定义的常量 和 计算 两种方式来显示各数据类型的实际取值范围。#include <stdio.h>
#include <limits.h>
#include <float.h>
int main()
{
//从标准头文件中输出
printf("The values from standard file:\n");
printf("------------------------------\n");
printf("signed char: %d ~ %d\n",SCHAR_MIN , SCHAR_MAX);
printf("unSigned char: %d ~ %u\n",0 , UCHAR_MAX);
printf("signed short: %d ~ %d\n",SHRT_MIN, SHRT_MAX);
printf("unSigned short: %d ~ %u\n",0 , UCHAR_MAX);
printf("signed int: %d ~ %d\n",INT_MIN, INT_MAX);
printf("unSigned int: %d ~ %u\n",0 , UCHAR_MAX);
printf("signed long: %ld ~ %ld\n",LONG_MIN , LONG_MAX);
printf("unSigned long: %d ~ %lu\n",0 , ULONG_MAX);
printf("------------------------------\n");
//直接计算
printf("The values from calculate:\n");
printf("------------------------------\n");
printf("signed char: %d ~ %d\n", -(char)((unsigned char) ~0 >> 1) - 1, (char)((unsigned char) ~0 >> 1));
printf("unSigned char: %d ~ %u\n",0 , (unsigned char) ~0);
printf("signed short: %d ~ %d\n",-(short)((unsigned short) ~0 >> 1) - 1, (short)((unsigned short) ~0 >> 1));
printf("unSigned short: %d ~ %u\n",0 , (unsigned short) ~0);
printf("signed int: %d ~ %d\n",-(int)((unsigned int) ~0 >> 1) - 1, (int)((unsigned int) ~0 >> 1));
printf("unSigned int: %d ~ %u\n",0 ,(unsigned int) ~0);
printf("signed long: %ld ~ %ld\n",-(long)((unsigned long) ~0 >> 1) - 1, (long)((unsigned long) ~0 >> 1));
printf("unSigned long: %d ~ %lu\n",0 ,(unsigned long) ~0);
//查看类型占用字节数
long long a;
printf("%ld", sizeof a);
return 0;
}#操作系统的情况
Windows 10 64位系统
Mac OS 64位系统
可以看到，char、short、int这三个类型的数据长度，在两个平台下的长度是一致的，但是long类型就不太一样了，明显mac上的取值范围更大，而且大很多~ 为什么呢？
我们都知道，类型的取值范围是多少，取决于其所占用的位数，那么两个平台，针对long类型，显然分配的位数是不同的。通过sizeof（对这个详细了解再总结吧），总之它是C/C++中的一个操作符（operator），简单的说其作用就是返回一个对象或者类型所占的内存字节数。所以，在程序中加入了下面的代码，查看下两个系统中long分别分配的内存字节数，就可以知道对应的位数了。
//查看类型占用字节数
long a;
printf("%ld", sizeof a);果然，在Windows下，输出结果是4，在mac下输出结果是8。换算成位数，也就是windows下是32位，mac下是64位。这就解释了为啥两个系统下的long类型取值范围为啥不相同了。
但是另外一个问题来了：为啥同样是64位系统，window下long就是32位，而Mac下是64位呢？经过查询资料，才发现其中的门道。
在Unix世界中，针对64位平台的整数和指针的大小有一些可能的安排。其中最常用的两个是ILP64（实际上，这只是其中的一小部分例子，Cray就是这样）和LP64（几乎所有其他的）。首字母来自'int，long，指针是64位'和'long，指针是64位'。
Type ILP64 LP64 LLP64
char 8 8 8
short 16 16 16
int 64 32 32
long 64 64 32
long long 64 64 64
pointer 64 64 64ILP64系统因LP64而被放弃（也就是说，几乎所有后来的进入者都使用LP64，这是基于Aspen小组的建议;只有具有64位操作悠久遗产的系统使用不同的方案）。所有现代的64位Unix系统都使用LP64。MacOS X和Linux都是现代64位系统。
Microsoft使用不同的方案转换为64位：LLP64（'long long，指针为64位'）。这意味着32位软件可以在不改变的情况下重新编译。它具有与其他人不同的缺点，还需要对代码进行修改以利用64位容量。总是需要修改; 它只是与Unix平台上需要的版本不同的修订版本。
这下可以解释了，为什么windows下的long类型是32位的，因为Microsoft针对64位系统，采用的是LLP64位的方案。在这方案里，long类型是32位，longlong类型才是64位。在windows的官方说明文档中，也可以查到相应的类型释义：
那么，我们把程序改一改，是不是就可以输出相同的结果了呢？答案，不置可否！修改后的程序如下：#include <stdio.h>
#include <limits.h>
#include <float.h>
int main()
{
//从标准头文件中输出
printf("The values from standard file:\n");
printf("------------------------------\n");
printf("signed char: %d ~ %d\n",SCHAR_MIN , SCHAR_MAX);
printf("unSigned char: %d ~ %u\n",0 , UCHAR_MAX);
printf("signed short: %d ~ %d\n",SHRT_MIN, SHRT_MAX);
printf("unSigned short: %d ~ %u\n",0 , UCHAR_MAX);
printf("signed int: %d ~ %d\n",INT_MIN, INT_MAX);
printf("unSigned int: %d ~ %u\n",0 , UCHAR_MAX);
printf("signed long: %lld ~ %lld\n",LONG_LONG_MIN , LONG_LONG_MAX);
printf("unSigned long: %d ~ %llu\n",0 , ULLONG_MAX);
printf("------------------------------\n");
//直接计算
printf("The values from calculate:\n");
printf("------------------------------\n");
printf("signed char: %d ~ %d\n", -(char)((unsigned char) ~0 >> 1) - 1, (char)((unsigned char) ~0 >> 1));
printf("unSigned char: %d ~ %u\n",0 , (unsigned char) ~0);
printf("signed short: %d ~ %d\n",-(short)((unsigned short) ~0 >> 1) - 1, (short)((unsigned short) ~0 >> 1));
printf("unSigned short: %d ~ %u\n",0 , (unsigned short) ~0);
printf("signed int: %d ~ %d\n",-(int)((unsigned int) ~0 >> 1) - 1, (int)((unsigned int) ~0 >> 1));
printf("unSigned int: %d ~ %u\n",0 ,(unsigned int) ~0);
printf("signed long: %lld ~ %lld\n",-(long long)((unsigned long long) ~0 >> 1) - 1, (long long)((unsigned long long) ~0 >> 1));
printf("unSigned long: %d ~ %llu\n",0 ,(unsigned long long) ~0);
//查看类型占用字节数
long long a;
printf("%ld", sizeof a);
return 0;
}主要看long类型，我们替换成了long long，它对应的头文件常量是：LONG_LONG_MIN、LONG_LONG_MAX和ULLONG_MAX。当然，输出这个长度的数据，要使用 %lld 和 %llu。否则数据输出会变小。
题外话：
首先要说的是，和Java等语言不同，C/C++本身并没有规定各数据类型的位数，只是限定了一个大小关系，也就是规定从所占的bit数来说，short <= int <= long <= long long。至于具体哪种类型占用多少位，是由你所用的开发平台的编译器决定的。在现在的PC上一个通常的标准是，int和long同为32位，long long为64位。但是如果换到其它平台(如ARM)上，这个数字可能会有不同，类型所占的大小可以用sizeof()运算符查看。
long long是C99标准中新引进的数据类型，在古老的VC6.0中并没有这个类型，所以在VC6.0中用”long long”会发生编译错误。为了表示64位整数，VC6里采用的是微软自己搞出来的一个数据类型，叫做__int64，所以如果你是在VC6.0下编译的话，应该用__int64定义64位整型。新版的Visual Studio已经支持long long了。GCC是支持long long的，我们在win系统中使用的其它IDE如Dev-Cpp, Code::Blocks等等大多是采用的MinGW编译环境，它是与GCC兼容的，所以也支持long long（另外为了与MS兼容，也支持__int64）。如果是在纯的linux下，就只能使用long long了。
关于使用printf的输入输出，这里就有一个更囧的情况。实际上只要记住，主要的区分在于操作系统：如果在win系统下，那么无论什么编译器，一律用%I64d；如果在linux系统，一律用%lld。这是因为MS提供的msvcrt.dll库里使用的就是%I64d的方式，尽管Dev-Cpp等在语法上支持标准，但也不得不使用MS提供的dll库来完成IO，所以就造成了这种情况。
参考文档：
https://docs.microsoft.com/zh-cn/windows/win32/winprog/windows-data-types
https://cloud.tencent.com/developer/ask/62686
https://blog.csdn.net/qq_31736627/article/details/52912691
查看全部
在今天的课堂任务中，相同的程序代码，在windows和Mac os两个平台下，编译执行之后的结果竟然不太一样，有点儿“奇怪”，想知道原因为何？所以进行了一番研究梳理！
首先看下代码源码：很简单，要求就是通过标准文件中定义的常量 和 计算 两种方式来显示各数据类型的实际取值范围。
可以看到，char、short、int这三个类型的数据长度，在两个平台下的长度是一致的，但是long类型就不太一样了，明显mac上的取值范围更大，而且大很多~ 为什么呢？
我们都知道，类型的取值范围是多少，取决于其所占用的位数，那么两个平台，针对long类型，显然分配的位数是不同的。通过sizeof（对这个详细了解再总结吧），总之它是C/C++中的一个操作符（operator），简单的说其作用就是返回一个对象或者类型所占的内存字节数。所以，在程序中加入了下面的代码，查看下两个系统中long分别分配的内存字节数，就可以知道对应的位数了。
但是另外一个问题来了：为啥同样是64位系统，window下long就是32位，而Mac下是64位呢？经过查询资料，才发现其中的门道。
在Unix世界中，针对64位平台的整数和指针的大小有一些可能的安排。其中最常用的两个是ILP64（实际上，这只是其中的一小部分例子，Cray就是这样）和LP64（几乎所有其他的）。首字母来自'int，long，指针是64位'和'long，指针是64位'。
Microsoft使用不同的方案转换为64位：LLP64（'long long，指针为64位'）。这意味着32位软件可以在不改变的情况下重新编译。它具有与其他人不同的缺点，还需要对代码进行修改以利用64位容量。总是需要修改; 它只是与Unix平台上需要的版本不同的修订版本。
这下可以解释了，为什么windows下的long类型是32位的，因为Microsoft针对64位系统，采用的是LLP64位的方案。在这方案里，long类型是32位，longlong类型才是64位。在windows的官方说明文档中，也可以查到相应的类型释义：
那么，我们把程序改一改，是不是就可以输出相同的结果了呢？答案，不置可否！修改后的程序如下：
题外话：
首先要说的是，和Java等语言不同，C/C++本身并没有规定各数据类型的位数，只是限定了一个大小关系，也就是规定从所占的bit数来说，short <= int <= long <= long long。至于具体哪种类型占用多少位，是由你所用的开发平台的编译器决定的。在现在的PC上一个通常的标准是，int和long同为32位，long long为64位。但是如果换到其它平台(如ARM)上，这个数字可能会有不同，类型所占的大小可以用sizeof()运算符查看。
long long是C99标准中新引进的数据类型，在古老的VC6.0中并没有这个类型，所以在VC6.0中用”long long”会发生编译错误。为了表示64位整数，VC6里采用的是微软自己搞出来的一个数据类型，叫做__int64，所以如果你是在VC6.0下编译的话，应该用__int64定义64位整型。新版的Visual Studio已经支持long long了。GCC是支持long long的，我们在win系统中使用的其它IDE如Dev-Cpp, Code::Blocks等等大多是采用的MinGW编译环境，它是与GCC兼容的，所以也支持long long（另外为了与MS兼容，也支持__int64）。如果是在纯的linux下，就只能使用long long了。
关于使用printf的输入输出，这里就有一个更囧的情况。实际上只要记住，主要的区分在于操作系统：如果在win系统下，那么无论什么编译器，一律用%I64d；如果在linux系统，一律用%lld。这是因为MS提供的msvcrt.dll库里使用的就是%I64d的方式，尽管Dev-Cpp等在语法上支持标准，但也不得不使用MS提供的dll库来完成IO，所以就造成了这种情况。
参考文档：
https://docs.microsoft.com/zh-cn/windows/win32/winprog/windows-data-types
https://cloud.tencent.com/developer/ask/62686
https://blog.csdn.net/qq_31736627/article/details/52912691
首先看下代码源码：很简单，要求就是通过标准文件中定义的常量 和 计算 两种方式来显示各数据类型的实际取值范围。
#include <stdio.h>
#include <limits.h>
#include <float.h>
int main()
{
//从标准头文件中输出
printf("The values from standard file:\n");
printf("------------------------------\n");
printf("signed char: %d ~ %d\n",SCHAR_MIN , SCHAR_MAX);
printf("unSigned char: %d ~ %u\n",0 , UCHAR_MAX);
printf("signed short: %d ~ %d\n",SHRT_MIN, SHRT_MAX);
printf("unSigned short: %d ~ %u\n",0 , UCHAR_MAX);
printf("signed int: %d ~ %d\n",INT_MIN, INT_MAX);
printf("unSigned int: %d ~ %u\n",0 , UCHAR_MAX);
printf("signed long: %ld ~ %ld\n",LONG_MIN , LONG_MAX);
printf("unSigned long: %d ~ %lu\n",0 , ULONG_MAX);
printf("------------------------------\n");
//直接计算
printf("The values from calculate:\n");
printf("------------------------------\n");
printf("signed char: %d ~ %d\n", -(char)((unsigned char) ~0 >> 1) - 1, (char)((unsigned char) ~0 >> 1));
printf("unSigned char: %d ~ %u\n",0 , (unsigned char) ~0);
printf("signed short: %d ~ %d\n",-(short)((unsigned short) ~0 >> 1) - 1, (short)((unsigned short) ~0 >> 1));
printf("unSigned short: %d ~ %u\n",0 , (unsigned short) ~0);
printf("signed int: %d ~ %d\n",-(int)((unsigned int) ~0 >> 1) - 1, (int)((unsigned int) ~0 >> 1));
printf("unSigned int: %d ~ %u\n",0 ,(unsigned int) ~0);
printf("signed long: %ld ~ %ld\n",-(long)((unsigned long) ~0 >> 1) - 1, (long)((unsigned long) ~0 >> 1));
printf("unSigned long: %d ~ %lu\n",0 ,(unsigned long) ~0);
//查看类型占用字节数
long long a;
printf("%ld", sizeof a);
return 0;
}
#操作系统的情况
Windows 10 64位系统
Mac OS 64位系统
可以看到，char、short、int这三个类型的数据长度，在两个平台下的长度是一致的，但是long类型就不太一样了，明显mac上的取值范围更大，而且大很多~ 为什么呢？
我们都知道，类型的取值范围是多少，取决于其所占用的位数，那么两个平台，针对long类型，显然分配的位数是不同的。通过sizeof（对这个详细了解再总结吧），总之它是C/C++中的一个操作符（operator），简单的说其作用就是返回一个对象或者类型所占的内存字节数。所以，在程序中加入了下面的代码，查看下两个系统中long分别分配的内存字节数，就可以知道对应的位数了。
//查看类型占用字节数果然，在Windows下，输出结果是4，在mac下输出结果是8。换算成位数，也就是windows下是32位，mac下是64位。这就解释了为啥两个系统下的long类型取值范围为啥不相同了。
long a;
printf("%ld", sizeof a);
但是另外一个问题来了：为啥同样是64位系统，window下long就是32位，而Mac下是64位呢？经过查询资料，才发现其中的门道。
在Unix世界中，针对64位平台的整数和指针的大小有一些可能的安排。其中最常用的两个是ILP64（实际上，这只是其中的一小部分例子，Cray就是这样）和LP64（几乎所有其他的）。首字母来自'int，long，指针是64位'和'long，指针是64位'。
Type ILP64 LP64 LLP64ILP64系统因LP64而被放弃（也就是说，几乎所有后来的进入者都使用LP64，这是基于Aspen小组的建议;只有具有64位操作悠久遗产的系统使用不同的方案）。所有现代的64位Unix系统都使用LP64。MacOS X和Linux都是现代64位系统。
char 8 8 8
short 16 16 16
int 64 32 32
long 64 64 32
long long 64 64 64
pointer 64 64 64
Microsoft使用不同的方案转换为64位：LLP64（'long long，指针为64位'）。这意味着32位软件可以在不改变的情况下重新编译。它具有与其他人不同的缺点，还需要对代码进行修改以利用64位容量。总是需要修改; 它只是与Unix平台上需要的版本不同的修订版本。
这下可以解释了，为什么windows下的long类型是32位的，因为Microsoft针对64位系统，采用的是LLP64位的方案。在这方案里，long类型是32位，longlong类型才是64位。在windows的官方说明文档中，也可以查到相应的类型释义：
那么，我们把程序改一改，是不是就可以输出相同的结果了呢？答案，不置可否！修改后的程序如下：
#include <stdio.h>主要看long类型，我们替换成了long long，它对应的头文件常量是：LONG_LONG_MIN、LONG_LONG_MAX和ULLONG_MAX。当然，输出这个长度的数据，要使用 %lld 和 %llu。否则数据输出会变小。
#include <limits.h>
#include <float.h>
int main()
{
//从标准头文件中输出
printf("The values from standard file:\n");
printf("------------------------------\n");
printf("signed char: %d ~ %d\n",SCHAR_MIN , SCHAR_MAX);
printf("unSigned char: %d ~ %u\n",0 , UCHAR_MAX);
printf("signed short: %d ~ %d\n",SHRT_MIN, SHRT_MAX);
printf("unSigned short: %d ~ %u\n",0 , UCHAR_MAX);
printf("signed int: %d ~ %d\n",INT_MIN, INT_MAX);
printf("unSigned int: %d ~ %u\n",0 , UCHAR_MAX);
printf("signed long: %lld ~ %lld\n",LONG_LONG_MIN , LONG_LONG_MAX);
printf("unSigned long: %d ~ %llu\n",0 , ULLONG_MAX);
printf("------------------------------\n");
//直接计算
printf("The values from calculate:\n");
printf("------------------------------\n");
printf("signed char: %d ~ %d\n", -(char)((unsigned char) ~0 >> 1) - 1, (char)((unsigned char) ~0 >> 1));
printf("unSigned char: %d ~ %u\n",0 , (unsigned char) ~0);
printf("signed short: %d ~ %d\n",-(short)((unsigned short) ~0 >> 1) - 1, (short)((unsigned short) ~0 >> 1));
printf("unSigned short: %d ~ %u\n",0 , (unsigned short) ~0);
printf("signed int: %d ~ %d\n",-(int)((unsigned int) ~0 >> 1) - 1, (int)((unsigned int) ~0 >> 1));
printf("unSigned int: %d ~ %u\n",0 ,(unsigned int) ~0);
printf("signed long: %lld ~ %lld\n",-(long long)((unsigned long long) ~0 >> 1) - 1, (long long)((unsigned long long) ~0 >> 1));
printf("unSigned long: %d ~ %llu\n",0 ,(unsigned long long) ~0);
//查看类型占用字节数
long long a;
printf("%ld", sizeof a);
return 0;
}
题外话：
首先要说的是，和Java等语言不同，C/C++本身并没有规定各数据类型的位数，只是限定了一个大小关系，也就是规定从所占的bit数来说，short <= int <= long <= long long。至于具体哪种类型占用多少位，是由你所用的开发平台的编译器决定的。在现在的PC上一个通常的标准是，int和long同为32位，long long为64位。但是如果换到其它平台(如ARM)上，这个数字可能会有不同，类型所占的大小可以用sizeof()运算符查看。
long long是C99标准中新引进的数据类型，在古老的VC6.0中并没有这个类型，所以在VC6.0中用”long long”会发生编译错误。为了表示64位整数，VC6里采用的是微软自己搞出来的一个数据类型，叫做__int64，所以如果你是在VC6.0下编译的话，应该用__int64定义64位整型。新版的Visual Studio已经支持long long了。GCC是支持long long的，我们在win系统中使用的其它IDE如Dev-Cpp, Code::Blocks等等大多是采用的MinGW编译环境，它是与GCC兼容的，所以也支持long long（另外为了与MS兼容，也支持__int64）。如果是在纯的linux下，就只能使用long long了。
关于使用printf的输入输出，这里就有一个更囧的情况。实际上只要记住，主要的区分在于操作系统：如果在win系统下，那么无论什么编译器，一律用%I64d；如果在linux系统，一律用%lld。这是因为MS提供的msvcrt.dll库里使用的就是%I64d的方式，尽管Dev-Cpp等在语法上支持标准，但也不得不使用MS提供的dll库来完成IO，所以就造成了这种情况。
参考文档：
https://docs.microsoft.com/zh-cn/windows/win32/winprog/windows-data-types
https://cloud.tencent.com/developer/ask/62686
https://blog.csdn.net/qq_31736627/article/details/52912691
#2020学习打卡##C程序设计语言# 原码、反码和补码
zkbhj 发表了文章 • 0 个评论 • 976 次浏览 • 2020-04-07 23:27
今天学习C程序设计语言的时候，遇到了一个概念，叫补码。其实这个概念在大学学习计算机基础的时候应该有学习过，但是还是基本上忘记的差不多了，需要重新补充回忆和学习一下。
一. 机器数和真值
在学习原码, 反码和补码之前, 需要先了解机器数和真值的概念.
1、机器数
一个数在计算机中的二进制表示形式, 叫做这个数的机器数。机器数是带符号的，在计算机用一个数的最高位存放符号, 正数为0, 负数为1.
比如，十进制中的数 +3 ，计算机字长为8位，转换成二进制就是00000011。如果是 -3 ，就是 10000011 。
那么，这里的 00000011 和 10000011 就是机器数。
2、真值
因为第一位是符号位，所以机器数的形式值就不等于真正的数值。例如上面的有符号数 10000011，其最高位1代表负，其真正数值是 -3 而不是形式值131（10000011转换成十进制等于131）。所以，为区别起见，将带符号位的机器数对应的真正数值称为机器数的真值。
例：0000 0001的真值 = +000 0001 = +1，1000 0001的真值 = –000 0001 = –1
二. 原码, 反码, 补码的基础概念和计算方法
在探求为何机器要使用补码之前, 让我们先了解原码, 反码和补码的概念.对于一个数, 计算机要使用一定的编码方式进行存储. 原码, 反码, 补码是机器存储一个具体数字的编码方式.
1. 原码
原码就是符号位加上真值的绝对值, 即用第一位表示符号, 其余位表示值. 比如如果是8位二进制:
[+1]原 = 0000 0001
[-1]原 = 1000 0001
第一位是符号位. 因为第一位是符号位, 所以8位二进制数的取值范围就是:
[1111 1111 , 0111 1111]
即
[-127 , 127]
原码是人脑最容易理解和计算的表示方式.
2. 反码
反码的表示方法是:
正数的反码是其本身
负数的反码是在其原码的基础上, 符号位不变，其余各个位取反.
[+1] = [00000001]原 = [00000001]反
[-1] = [10000001]原 = [11111110]反
可见如果一个反码表示的是负数, 人脑无法直观的看出来它的数值. 通常要将其转换成原码再计算.
3. 补码
补码的表示方法是:
正数的补码就是其本身
负数的补码是在其原码的基础上, 符号位不变, 其余各位取反, 最后+1. (即在反码的基础上+1)
[+1] = [00000001]原 = [00000001]反 = [00000001]补
[-1] = [10000001]原 = [11111110]反 = [11111111]补
对于负数, 补码表示方式也是人脑无法直观看出其数值的. 通常也需要转换成原码在计算其数值.
三. 为何要使用原码, 反码和补码
在开始深入学习前, 我的学习建议是先"死记硬背"上面的原码, 反码和补码的表示方式以及计算方法.
现在我们知道了计算机可以有三种编码方式表示一个数. 对于正数因为三种编码方式的结果都相同:
[+1] = [00000001]原 = [00000001]反 = [00000001]补
所以不需要过多解释. 但是对于负数:
[-1] = [10000001]原 = [11111110]反 = [11111111]补
可见原码, 反码和补码是完全不同的. 既然原码才是被人脑直接识别并用于计算表示方式, 为何还会有反码和补码呢?
首先, 因为人脑可以知道第一位是符号位, 在计算的时候我们会根据符号位, 选择对真值区域的加减. (真值的概念在本文最开头). 但是对于计算机, 加减乘数已经是最基础的运算, 要设计的尽量简单. 计算机辨别"符号位"显然会让计算机的基础电路设计变得十分复杂! 于是人们想出了将符号位也参与运算的方法. 我们知道, 根据运算法则减去一个正数等于加上一个负数, 即: 1-1 = 1 + (-1) = 0 , 所以机器可以只有加法而没有减法, 这样计算机运算的设计就更简单了.
于是人们开始探索 将符号位参与运算, 并且只保留加法的方法. 首先来看原码:
计算十进制的表达式: 1-1=0
1 - 1 = 1 + (-1) = [00000001]原 + [10000001]原 = [10000010]原 = -2
如果用原码表示, 让符号位也参与计算, 显然对于减法来说, 结果是不正确的.这也就是为何计算机内部不使用原码表示一个数.
为了解决原码做减法的问题, 出现了反码:
计算十进制的表达式: 1-1=0
1 - 1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原= [0000 0001]反 + [1111 1110]反 = [1111 1111]反 = [1000 0000]原 = -0
发现用反码计算减法, 结果的真值部分是正确的. 而唯一的问题其实就出现在"0"这个特殊的数值上. 虽然人们理解上+0和-0是一样的, 但是0带符号是没有任何意义的. 而且会有[0000 0000]原和[1000 0000]原两个编码表示0.
于是补码的出现, 解决了0的符号以及两个编码的问题:
1-1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原 = [0000 0001]补 + [1111 1111]补 = [0000 0000]补=[0000 0000]原
这样0用[0000 0000]表示, 而以前出现问题的-0则不存在了.而且可以用[1000 0000]表示-128:
(-1) + (-127) = [1000 0001]原 + [1111 1111]原 = [1111 1111]补 + [1000 0001]补 = [1000 0000]补
-1-127的结果应该是-128, 在用补码运算的结果中, [1000 0000]补 就是-128. 但是注意因为实际上是使用以前的-0的补码来表示-128, 所以-128并没有原码和反码表示.(对-128的补码表示[1000 0000]补算出来的原码是[0000 0000]原, 这是不正确的)
使用补码, 不仅仅修复了0的符号以及存在两个编码的问题, 而且还能够多表示一个最低数. 这就是为什么8位二进制, 使用原码或反码表示的范围为[-127, +127], 而使用补码表示的范围为[-128, 127].
因为机器使用补码, 所以对于编程中常用到的32位int类型, 可以表示范围是: [-231, 231-1] 因为第一位表示的是符号位.而使用补码表示时又可以多保存一个最小值.
数学概念和求证：
https://blog.csdn.net/zl10086111/article/details/80907428
查看全部
一. 机器数和真值
在学习原码, 反码和补码之前, 需要先了解机器数和真值的概念.
1、机器数
一个数在计算机中的二进制表示形式, 叫做这个数的机器数。机器数是带符号的，在计算机用一个数的最高位存放符号, 正数为0, 负数为1.
比如，十进制中的数 +3 ，计算机字长为8位，转换成二进制就是00000011。如果是 -3 ，就是 10000011 。
那么，这里的 00000011 和 10000011 就是机器数。
2、真值
因为第一位是符号位，所以机器数的形式值就不等于真正的数值。例如上面的有符号数 10000011，其最高位1代表负，其真正数值是 -3 而不是形式值131（10000011转换成十进制等于131）。所以，为区别起见，将带符号位的机器数对应的真正数值称为机器数的真值。
例：0000 0001的真值 = +000 0001 = +1，1000 0001的真值 = –000 0001 = –1
二. 原码, 反码, 补码的基础概念和计算方法
在探求为何机器要使用补码之前, 让我们先了解原码, 反码和补码的概念.对于一个数, 计算机要使用一定的编码方式进行存储. 原码, 反码, 补码是机器存储一个具体数字的编码方式.
1. 原码
原码就是符号位加上真值的绝对值, 即用第一位表示符号, 其余位表示值. 比如如果是8位二进制:
[+1]原 = 0000 0001
[-1]原 = 1000 0001
第一位是符号位. 因为第一位是符号位, 所以8位二进制数的取值范围就是:
[1111 1111 , 0111 1111]
即
[-127 , 127]
原码是人脑最容易理解和计算的表示方式.
2. 反码
反码的表示方法是:
正数的反码是其本身
负数的反码是在其原码的基础上, 符号位不变，其余各个位取反.
[+1] = [00000001]原 = [00000001]反
[-1] = [10000001]原 = [11111110]反
可见如果一个反码表示的是负数, 人脑无法直观的看出来它的数值. 通常要将其转换成原码再计算.
3. 补码
补码的表示方法是:
正数的补码就是其本身
负数的补码是在其原码的基础上, 符号位不变, 其余各位取反, 最后+1. (即在反码的基础上+1)
[+1] = [00000001]原 = [00000001]反 = [00000001]补
[-1] = [10000001]原 = [11111110]反 = [11111111]补
对于负数, 补码表示方式也是人脑无法直观看出其数值的. 通常也需要转换成原码在计算其数值.
三. 为何要使用原码, 反码和补码
在开始深入学习前, 我的学习建议是先"死记硬背"上面的原码, 反码和补码的表示方式以及计算方法.
现在我们知道了计算机可以有三种编码方式表示一个数. 对于正数因为三种编码方式的结果都相同:
[+1] = [00000001]原 = [00000001]反 = [00000001]补
所以不需要过多解释. 但是对于负数:
[-1] = [10000001]原 = [11111110]反 = [11111111]补
可见原码, 反码和补码是完全不同的. 既然原码才是被人脑直接识别并用于计算表示方式, 为何还会有反码和补码呢?
首先, 因为人脑可以知道第一位是符号位, 在计算的时候我们会根据符号位, 选择对真值区域的加减. (真值的概念在本文最开头). 但是对于计算机, 加减乘数已经是最基础的运算, 要设计的尽量简单. 计算机辨别"符号位"显然会让计算机的基础电路设计变得十分复杂! 于是人们想出了将符号位也参与运算的方法. 我们知道, 根据运算法则减去一个正数等于加上一个负数, 即: 1-1 = 1 + (-1) = 0 , 所以机器可以只有加法而没有减法, 这样计算机运算的设计就更简单了.
于是人们开始探索 将符号位参与运算, 并且只保留加法的方法. 首先来看原码:
计算十进制的表达式: 1-1=0
1 - 1 = 1 + (-1) = [00000001]原 + [10000001]原 = [10000010]原 = -2
如果用原码表示, 让符号位也参与计算, 显然对于减法来说, 结果是不正确的.这也就是为何计算机内部不使用原码表示一个数.
为了解决原码做减法的问题, 出现了反码:
计算十进制的表达式: 1-1=0
1 - 1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原= [0000 0001]反 + [1111 1110]反 = [1111 1111]反 = [1000 0000]原 = -0
发现用反码计算减法, 结果的真值部分是正确的. 而唯一的问题其实就出现在"0"这个特殊的数值上. 虽然人们理解上+0和-0是一样的, 但是0带符号是没有任何意义的. 而且会有[0000 0000]原和[1000 0000]原两个编码表示0.
于是补码的出现, 解决了0的符号以及两个编码的问题:
1-1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原 = [0000 0001]补 + [1111 1111]补 = [0000 0000]补=[0000 0000]原
这样0用[0000 0000]表示, 而以前出现问题的-0则不存在了.而且可以用[1000 0000]表示-128:
(-1) + (-127) = [1000 0001]原 + [1111 1111]原 = [1111 1111]补 + [1000 0001]补 = [1000 0000]补
-1-127的结果应该是-128, 在用补码运算的结果中, [1000 0000]补 就是-128. 但是注意因为实际上是使用以前的-0的补码来表示-128, 所以-128并没有原码和反码表示.(对-128的补码表示[1000 0000]补算出来的原码是[0000 0000]原, 这是不正确的)
使用补码, 不仅仅修复了0的符号以及存在两个编码的问题, 而且还能够多表示一个最低数. 这就是为什么8位二进制, 使用原码或反码表示的范围为[-127, +127], 而使用补码表示的范围为[-128, 127].
因为机器使用补码, 所以对于编程中常用到的32位int类型, 可以表示范围是: [-231, 231-1] 因为第一位表示的是符号位.而使用补码表示时又可以多保存一个最小值.
数学概念和求证：
https://blog.csdn.net/zl10086111/article/details/80907428
查看全部
今天学习C程序设计语言的时候，遇到了一个概念，叫补码。其实这个概念在大学学习计算机基础的时候应该有学习过，但是还是基本上忘记的差不多了，需要重新补充回忆和学习一下。
一. 机器数和真值
在学习原码, 反码和补码之前, 需要先了解机器数和真值的概念.
1、机器数
一个数在计算机中的二进制表示形式, 叫做这个数的机器数。机器数是带符号的，在计算机用一个数的最高位存放符号, 正数为0, 负数为1.
比如，十进制中的数 +3 ，计算机字长为8位，转换成二进制就是00000011。如果是 -3 ，就是 10000011 。
那么，这里的 00000011 和 10000011 就是机器数。
2、真值
因为第一位是符号位，所以机器数的形式值就不等于真正的数值。例如上面的有符号数 10000011，其最高位1代表负，其真正数值是 -3 而不是形式值131（10000011转换成十进制等于131）。所以，为区别起见，将带符号位的机器数对应的真正数值称为机器数的真值。
例：0000 0001的真值 = +000 0001 = +1，1000 0001的真值 = –000 0001 = –1
二. 原码, 反码, 补码的基础概念和计算方法
在探求为何机器要使用补码之前, 让我们先了解原码, 反码和补码的概念.对于一个数, 计算机要使用一定的编码方式进行存储. 原码, 反码, 补码是机器存储一个具体数字的编码方式.
1. 原码
原码就是符号位加上真值的绝对值, 即用第一位表示符号, 其余位表示值. 比如如果是8位二进制:
[+1]原 = 0000 0001
[-1]原 = 1000 0001
第一位是符号位. 因为第一位是符号位, 所以8位二进制数的取值范围就是:
[1111 1111 , 0111 1111]
即
[-127 , 127]
原码是人脑最容易理解和计算的表示方式.
2. 反码
反码的表示方法是:
正数的反码是其本身
负数的反码是在其原码的基础上, 符号位不变，其余各个位取反.
[+1] = [00000001]原 = [00000001]反
[-1] = [10000001]原 = [11111110]反
可见如果一个反码表示的是负数, 人脑无法直观的看出来它的数值. 通常要将其转换成原码再计算.
3. 补码
补码的表示方法是:
正数的补码就是其本身
负数的补码是在其原码的基础上, 符号位不变, 其余各位取反, 最后+1. (即在反码的基础上+1)
[+1] = [00000001]原 = [00000001]反 = [00000001]补
[-1] = [10000001]原 = [11111110]反 = [11111111]补
对于负数, 补码表示方式也是人脑无法直观看出其数值的. 通常也需要转换成原码在计算其数值.
三. 为何要使用原码, 反码和补码
在开始深入学习前, 我的学习建议是先"死记硬背"上面的原码, 反码和补码的表示方式以及计算方法.
现在我们知道了计算机可以有三种编码方式表示一个数. 对于正数因为三种编码方式的结果都相同:
[+1] = [00000001]原 = [00000001]反 = [00000001]补
所以不需要过多解释. 但是对于负数:
[-1] = [10000001]原 = [11111110]反 = [11111111]补
可见原码, 反码和补码是完全不同的. 既然原码才是被人脑直接识别并用于计算表示方式, 为何还会有反码和补码呢?
首先, 因为人脑可以知道第一位是符号位, 在计算的时候我们会根据符号位, 选择对真值区域的加减. (真值的概念在本文最开头). 但是对于计算机, 加减乘数已经是最基础的运算, 要设计的尽量简单. 计算机辨别"符号位"显然会让计算机的基础电路设计变得十分复杂! 于是人们想出了将符号位也参与运算的方法. 我们知道, 根据运算法则减去一个正数等于加上一个负数, 即: 1-1 = 1 + (-1) = 0 , 所以机器可以只有加法而没有减法, 这样计算机运算的设计就更简单了.
于是人们开始探索 将符号位参与运算, 并且只保留加法的方法. 首先来看原码:
计算十进制的表达式: 1-1=0
1 - 1 = 1 + (-1) = [00000001]原 + [10000001]原 = [10000010]原 = -2
如果用原码表示, 让符号位也参与计算, 显然对于减法来说, 结果是不正确的.这也就是为何计算机内部不使用原码表示一个数.
为了解决原码做减法的问题, 出现了反码:
计算十进制的表达式: 1-1=0
1 - 1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原= [0000 0001]反 + [1111 1110]反 = [1111 1111]反 = [1000 0000]原 = -0
发现用反码计算减法, 结果的真值部分是正确的. 而唯一的问题其实就出现在"0"这个特殊的数值上. 虽然人们理解上+0和-0是一样的, 但是0带符号是没有任何意义的. 而且会有[0000 0000]原和[1000 0000]原两个编码表示0.
于是补码的出现, 解决了0的符号以及两个编码的问题:
1-1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原 = [0000 0001]补 + [1111 1111]补 = [0000 0000]补=[0000 0000]原
这样0用[0000 0000]表示, 而以前出现问题的-0则不存在了.而且可以用[1000 0000]表示-128:
(-1) + (-127) = [1000 0001]原 + [1111 1111]原 = [1111 1111]补 + [1000 0001]补 = [1000 0000]补
-1-127的结果应该是-128, 在用补码运算的结果中, [1000 0000]补 就是-128. 但是注意因为实际上是使用以前的-0的补码来表示-128, 所以-128并没有原码和反码表示.(对-128的补码表示[1000 0000]补算出来的原码是[0000 0000]原, 这是不正确的)
因为机器使用补码, 所以对于编程中常用到的32位int类型, 可以表示范围是: [-231, 231-1] 因为第一位表示的是符号位.而使用补码表示时又可以多保存一个最小值.
数学概念和求证：
https://blog.csdn.net/zl10086111/article/details/80907428
一. 机器数和真值
在学习原码, 反码和补码之前, 需要先了解机器数和真值的概念.
1、机器数
一个数在计算机中的二进制表示形式, 叫做这个数的机器数。机器数是带符号的，在计算机用一个数的最高位存放符号, 正数为0, 负数为1.
比如，十进制中的数 +3 ，计算机字长为8位，转换成二进制就是00000011。如果是 -3 ，就是 10000011 。
那么，这里的 00000011 和 10000011 就是机器数。
2、真值
因为第一位是符号位，所以机器数的形式值就不等于真正的数值。例如上面的有符号数 10000011，其最高位1代表负，其真正数值是 -3 而不是形式值131（10000011转换成十进制等于131）。所以，为区别起见，将带符号位的机器数对应的真正数值称为机器数的真值。
例：0000 0001的真值 = +000 0001 = +1，1000 0001的真值 = –000 0001 = –1
二. 原码, 反码, 补码的基础概念和计算方法
在探求为何机器要使用补码之前, 让我们先了解原码, 反码和补码的概念.对于一个数, 计算机要使用一定的编码方式进行存储. 原码, 反码, 补码是机器存储一个具体数字的编码方式.
1. 原码
原码就是符号位加上真值的绝对值, 即用第一位表示符号, 其余位表示值. 比如如果是8位二进制:
[+1]原 = 0000 0001
[-1]原 = 1000 0001
第一位是符号位. 因为第一位是符号位, 所以8位二进制数的取值范围就是:
[1111 1111 , 0111 1111]
即
[-127 , 127]
原码是人脑最容易理解和计算的表示方式.
2. 反码
反码的表示方法是:
正数的反码是其本身
负数的反码是在其原码的基础上, 符号位不变，其余各个位取反.
[+1] = [00000001]原 = [00000001]反
[-1] = [10000001]原 = [11111110]反
可见如果一个反码表示的是负数, 人脑无法直观的看出来它的数值. 通常要将其转换成原码再计算.
3. 补码
补码的表示方法是:
正数的补码就是其本身
负数的补码是在其原码的基础上, 符号位不变, 其余各位取反, 最后+1. (即在反码的基础上+1)
[+1] = [00000001]原 = [00000001]反 = [00000001]补
[-1] = [10000001]原 = [11111110]反 = [11111111]补
对于负数, 补码表示方式也是人脑无法直观看出其数值的. 通常也需要转换成原码在计算其数值.
三. 为何要使用原码, 反码和补码
在开始深入学习前, 我的学习建议是先"死记硬背"上面的原码, 反码和补码的表示方式以及计算方法.
现在我们知道了计算机可以有三种编码方式表示一个数. 对于正数因为三种编码方式的结果都相同:
[+1] = [00000001]原 = [00000001]反 = [00000001]补
所以不需要过多解释. 但是对于负数:
[-1] = [10000001]原 = [11111110]反 = [11111111]补
可见原码, 反码和补码是完全不同的. 既然原码才是被人脑直接识别并用于计算表示方式, 为何还会有反码和补码呢?
首先, 因为人脑可以知道第一位是符号位, 在计算的时候我们会根据符号位, 选择对真值区域的加减. (真值的概念在本文最开头). 但是对于计算机, 加减乘数已经是最基础的运算, 要设计的尽量简单. 计算机辨别"符号位"显然会让计算机的基础电路设计变得十分复杂! 于是人们想出了将符号位也参与运算的方法. 我们知道, 根据运算法则减去一个正数等于加上一个负数, 即: 1-1 = 1 + (-1) = 0 , 所以机器可以只有加法而没有减法, 这样计算机运算的设计就更简单了.
于是人们开始探索 将符号位参与运算, 并且只保留加法的方法. 首先来看原码:
计算十进制的表达式: 1-1=0
1 - 1 = 1 + (-1) = [00000001]原 + [10000001]原 = [10000010]原 = -2
如果用原码表示, 让符号位也参与计算, 显然对于减法来说, 结果是不正确的.这也就是为何计算机内部不使用原码表示一个数.
为了解决原码做减法的问题, 出现了反码:
计算十进制的表达式: 1-1=0
1 - 1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原= [0000 0001]反 + [1111 1110]反 = [1111 1111]反 = [1000 0000]原 = -0
发现用反码计算减法, 结果的真值部分是正确的. 而唯一的问题其实就出现在"0"这个特殊的数值上. 虽然人们理解上+0和-0是一样的, 但是0带符号是没有任何意义的. 而且会有[0000 0000]原和[1000 0000]原两个编码表示0.
于是补码的出现, 解决了0的符号以及两个编码的问题:
1-1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原 = [0000 0001]补 + [1111 1111]补 = [0000 0000]补=[0000 0000]原
这样0用[0000 0000]表示, 而以前出现问题的-0则不存在了.而且可以用[1000 0000]表示-128:
(-1) + (-127) = [1000 0001]原 + [1111 1111]原 = [1111 1111]补 + [1000 0001]补 = [1000 0000]补
-1-127的结果应该是-128, 在用补码运算的结果中, [1000 0000]补 就是-128. 但是注意因为实际上是使用以前的-0的补码来表示-128, 所以-128并没有原码和反码表示.(对-128的补码表示[1000 0000]补算出来的原码是[0000 0000]原, 这是不正确的)
使用补码, 不仅仅修复了0的符号以及存在两个编码的问题, 而且还能够多表示一个最低数. 这就是为什么8位二进制, 使用原码或反码表示的范围为[-127, +127], 而使用补码表示的范围为[-128, 127].
因为机器使用补码, 所以对于编程中常用到的32位int类型, 可以表示范围是: [-231, 231-1] 因为第一位表示的是符号位.而使用补码表示时又可以多保存一个最小值.
数学概念和求证：
https://blog.csdn.net/zl10086111/article/details/80907428